Drill Cuttings Transportation in Deviated Wells

Introduction

A scientifically justified program to drill and clean the wellbore from the resulting cuttings makes it possible to significantly reduce the time and costs associated with drilling due to the geological and technological risks.

To choose the optimal set of conditions, it is necessary to have the appropriate mathematical modeling tools, based on modern computation algorithms, as well as physical models of the processes that occur during drilling.

This paper presents the results of calculations performed, for various conditions, under which drill cuttings are removed from deviated wells using the software developed by the authors.

A one-dimensional non-stationary thermal non-equilibrium mathematical model has been developed for modeling the removal of drill cuttings during the drilling of vertical, horizontal, and inclined wells. The model simulates the movement of the fluid and the cuttings particles, as well as the deposition of these particles and the formation of a stationary effective mud sheath (bed) (Fig. 1). The fluid rheology can be either Newtonian or non-Newtonian. The heat exchange between the cuttings, the fluid, and the wellbore walls is also considered. The following parameters are taken as inputs to the model: concentration (source) of the cuttings at the inlet; pressure (flow rate) at the inlet and at the outlet; temperature of the cuttings, the fluid and the reservoir rocks; drill bit speed; wellbore inclination angle relative to the horizontal. The model’s outputs are: pressure distribution, temperatures of the cuttings and the fluid, cuttings concentrations and bed areas along the wellbore surface at different points in times. It is possible to model the repeated removal and deposition of the cuttings particles from the wellbore. 

Mathematical Model

The two-layer model studied in [1,2] assumes that the upper layer corresponds to fluid with particles suspended in it. The lower layer corresponds to a stationary bed formed by deposited cuttings particles. For each layer, the mass, energy, and momentum conservation equations are set down for each component thereof, viz. cuttings or fluid. Notice that the concentration of particles suspended in the flow and the thickness of the stationary bed vary due to the deposition of cuttings onto the bed and the entrainment thereof from the bed.

The velocity of solid particles in the liquid phase and the velocity of the liquid phase can be found by solving the respective momentum conservation equations. Notice that the momentum of the system may change depending on the effects of gravitational forces, on the particles’ friction against the fluid flow, against the stationary bed, or against the channel walls, as well as on the deposition and transport of the particles.

In this paper it is also assumed that the bed is stationary. This is true for drilling speeds between 50 and 400 m/s for medium (3–7 mm) and relatively large (>7 mm) cuttings particle sizes.

Friction against the channel wall, as well as friction between the cuttings particles and the drilling fluid, is calculated based on the ratios set forth, e. g., in [3,4].

The approach used to describe how the drill string rotation speed affects cutting transport is indicated in [2].

Knowing the pressure distribution along the wellbore column, it is possible to calculate the equivalent circulating density  ρ as a function of time:

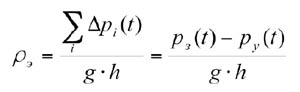
here 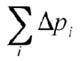   is the total loss of pressure in the annulus; g is the gravitational acceleration; h is the vertical depth; p₃ is the downhole pressure; p_y is the wellhead pressure.

Modeling the cuttings movement in an inclined well – Formulating the problem

To demonstrate the adequacy of the mathematical model for removing the non-stationary cuttings transport calculations, a realistic model of an inclined well was formulated (Fig. 2–3).

Considering the wellbore geometry, it is necessary to construct an analytical model of the well comprising a series of interconnected elements (channels). Each channel simulates a specific wellbore section characterized by a specific inclination angle relative to the horizontal and a specific geometry. The rotation of the drill bit is also considered. The parameters of each channel are set forth in Table 1.

The outputs of the created well model at different rates of penetration and connection times were used to describe the cuttings removal and equivalent circulating density as functions of time. Here, the drill time is determined by the rate of penetration per pipe segment of a given length. The length of said segment was assumed to be 10 m. Additionally, with a view to studying how the cuttings particle size affects the resulting ECD values, the particle diameter was assumed to be 9 mm at penetration rates of 5–150 m/h (drilling with roller-cone bits) and 3 mm at 200–400 m/h (for polycrystalline diamond compact (PDC) bits). These parameters were fur-ther used in modeling (Table 2).

The peculiar dependence of the rate of penetration on time is shown in Fig. 4. The parameters used to define the boundary conditions were the mass of cuttings transported per unit time, the downhole drilling fluid flow rate, and the pressure at the wellhead. The mass of cuttings transported per unit time is determined based on the rate of penetration, as shown in the expression below:

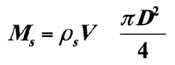
here V is the rate of penetration, D is the outer wellbore diameter.

The drilling fluid flow rate through the drill string was assumed to be 35 l/s. The rock density was assumed to
be equal ρ_s = 2.3 g/cm³, and the drilling fluid density – 1.25 g/cm³. Newtonian rheology was assumed. It was also assumed that the cuttings particles have a spherical shape, and their diameter was assumed to be equal d_s = 3 mm (for rates of penetration 200–400 m/h) or 9 mm (for rates lower than 200 m/h).

Computation Results

The dependence of the equivalent circulating density (ECD) on time relative to the drilling fluid density at a penetration rate of 50 m/h is shown in Fig. 5. The initial growth of the ECD is associated with an increased mass of cuttings in the flow, as a result of drilling. The dips correspond to pipe connection operations, during which the drilling and cleaning processes stop. After a certain time, the ECD value reaches a stationary phase, which corresponds to a dynamic equilibrium in which the volume of cuttings transported becomes equal to the amount of cuttings formed as a result of drilling. The stopping vs. drilling difference in the ECD values is determined by the difference in pressure loss due to the friction of the drilling fluid against the wellbore walls.

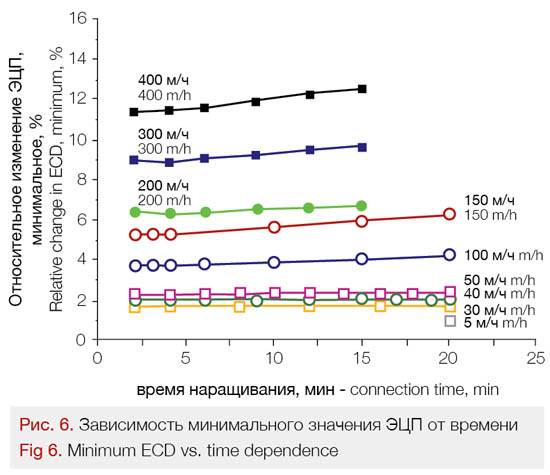
Fig. 6 shows the time dependence of the increase in the minimum steady-state ECD value relative to the drilling fluid density at different rates of penetration. Dependence of the relative maximum ECD value on the connection time at different rates of penetration is shown in Fig. 7.

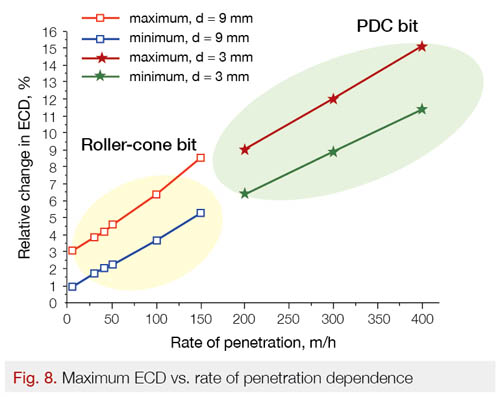
As can be seen in Fig. 6 and 7, the minimum and maximum relative ECD values also enter a stationary phase. Fig. 8 shows the dependence of the steady-state relative ECD value at different rates of penetration. It should be noted that for different rates of penetration, the rate of change in the ECD will be different.

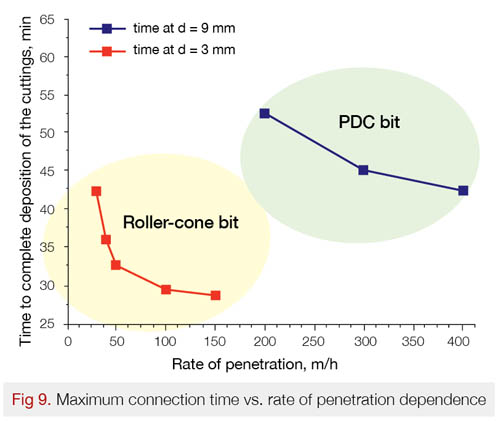
During the model’s construction, it was also determined that for each rate of penetration value, there is a maximum connection time at which the flow area formed between the drill string and the wellbore is completely clogged by the deposition of cuttings particles. The dependence of the connection time, at which the flow area clogging occurs, on the rate of penetration is shown in Fig. 9. The red line shows this dependence for cuttings particles taken to be 9 mm in size (the rate of penetration being 5–150 m/h), and the blue line – for those taken to be 3 mm in size (the rate of penetration being 200–400 m/h). Since particles with a diameter of 9 mm are heavier than 3-mm particles, their deposition time is much shorter. Just as expected, the higher the rate of penetration, the greater the amount of cuttings formed during drilling and, hence, the lower the maximum value of the connection time. value as a function of the mechanical penetration rate.

The ECD distribution along the wellbore was also calculated, taking into account the non-stationary effects of cuttings transportation, at different mechanical penetration rates. ECD computations were carried out as shown in [5], taking into account the change in the flow regime in the annulus; also obtained was a dependence of the change in the ECD value as a function of the mechanical penetration rate.

Fig. 10 shows the ECD distribution as a function of depth. The red curve shows the density of the drilling fluid; the blue curve shows the ECD distribution as a function of depth; the green curves show the distribution of the minimum average ECD value at rates of penetration between 50 and 200 m/h; the pink curve shows the distribution of the maximum average ECD value at rates of penetration between 50 and 200 m/h. Obviously, as the mechanical penetration rate increases, bottom hole mud accumulation begins to accelerate, thereby causing a local increase in the ECD value. It is, thus, necessary to ensure a high accuracy in determining the timing for making a connection and to perform the well cleanout routines more frequently, otherwise there is a high risk of loss of circulation.

Conclusion

The nonstationary mathematical model developed by the authors of this paper to describe the movement of drill cuttings in the wellbore has been used to carry out demonstrative computations for the displacement of cuttings by drilling fluid in an inclined well. Based on the actual grain size distribution in drill cuttings, two types of computations have been carried out, one for particles with a diameter of 9 mm (drilling with a roller-cone bit) and one for 3-mm particles (drilling with a PDC bit). It has been shown that the relative change in the ECD value, depending on the mechanical penetration rate, may increase up to 15%. The dependence between the mechanical penetration rate and the minimum time to complete deposition of the cuttings has been obtained to support the choice of connection time. It has been shown that the model makes it possible to adequately predict the time dependence of the ECD value, including that observed at high rates of penetration (200–400 m/h).

Bibliography

1. Q. T. Doan, M. Oguztoreli, Y. Masuda et al. Modeling of Transient Cuttings Transport in Underbalanced Drilling (UBD) // SPE Journal, 2003, v. 2, i. 2, p. 160–170;

2. S. Naganawa, T. Nomuro. Simulating transient behavior of cuttings transport over whole trajectory of extended-reach well // Society of Petroleum Engineers. IADC/SPE 103923. Asia Pacific Drilling Technology Conference and Exhibition, 2006, p. 1–9;

3. M. R. Malin. Turbulent pipe flow of Herschel-Bulkley fluids // International Communications in Heat and Mass Transfer, 1998, v. 25, i. 3, p. 321–330;

4. J. P. Hartnett, B. K. Rao. Heat transfer and pressure drop for purely viscous non-Newtonian fluids in turbulent flow through rectangular passages // Heat and Mass Transfer, 1987, v. 21, i. 5, p. 261–267;

5. N. R. Rabinovich. Engineering problems of continuum mechanics while drilling. – Moscow: Nedra, 1989, –, 270 p.: ill.:) ISBN 5-247-01587-8.

Authors

P. A. Lykhin¹, V. I. Chukhno², E. V. Usov², R. Z. Kurmangliyev¹, ,V. Ulyanov¹, E. Lukyanov³, N. Kayurov³

1 – Novosibirsk STC LLC

2 – Novosibirsk Branch, Nuclear Safety Institute (IBRAE) Russian Academy of Sciences 

3 – SPE «Looch»