Tim’s Theorem: A New Paradigm for Underground Hydrodynamics Part 1

“On nonlocality of Reasons”

“Isolated systems do not exist, and all systems even split by huge distances into parts with no signals, fields, mechanical forces, energy, etc. between them function like a consistent System”.

John Stuart Bell

1928 – 1990.

The article continues the publications [1, 5, 8…11], and supplies answers to the questions about pressure loss, influx during fluid filtration in zonally heterogeneous beds, proportionality factors for basic hydrodynamic parameters as well as the interrelation and interdependency between major hydrodynamic parameters of zonally heterogeneous beds. These questions were asked by the readers of the articles and attendees of conferences [3, 5, 6, 9]. On this basis we set out more clearly the formulas and calculations of bottom-hole pressure (BHP) loss ΔР_s, skin-factor formulas (S) and other basic hydrodynamic parameters of zonally heterogeneous beds.

“Tim’s Theorem” says that “Any changes of productive formation permeability lead to proportional changes in its productivity, hydroconductivity, BHP, dynamic fluid level, current influx and production potential, and their dimensionless relative values are equal to each other”.

“Productive formation – well – pumping (tubing) equipment” is a unified, inseparable hydrodynamic system, interrelated by fundamental dependencies that reflect the unity and interrelation of all hydrodynamic system parameters [4] (hereinafter: the system).

Tim’s Theorem is based on the three fundamental interrelated laws of subsurface hydrodynamics:

1. law on proportionality of basic hydrodynamic parameters of the system [1, 2].

The skin-factor value S is used here.

2. law on unity, interrelation and interdependency of basic hydrodynamic parameters of the system [3], (there is no parameters of the system that functions separately except independent variables Р_пл and k,);

3. law on mutual equality of relative values of basic hydrodynamic system parameters [5].

1. Developing a formula to calculate pressure loss ΔР_k in the process of fluid filtration into the wellbore

1.1. Analytical development of the formula for calculation of the pressure loss ΔР_k in the process of fluid filtration (Fig. 1.1).

To obtain this formula let us consider some uniform productive formations around the borehole wall which will, for the sake of discussion, have a  formation permeability factor k, external boundary R_к, formation pressure Р_пл and formation thickness h (Fig. 1.1).

Within the formation, let us select some annular level with r radius and dr thickness limited by surfaces with uniform permeability k. Direction of the fluid filtration is radial. According to the linear filtration law the total volume of fluid influx Q through the area unit F is equal to

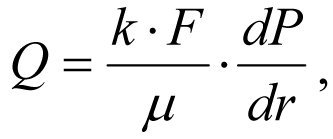 ,     (1.1)  where k is the permeability

factor; F is the fluid filtration area, F=2πrh;  μ is the dynamic viscosity of formation fluid; dP/dr is the radial gradient of pressure. Let us rewrite the equation (1.1) like this:

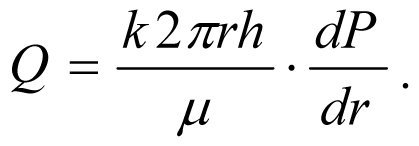   ,   (1.2) After division of variables we

will obtain the following:

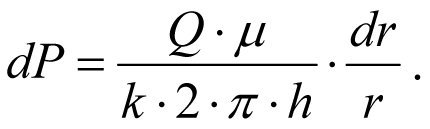   ,   (1.3) Integrating this equation gives

the following –

  ,  (1.4) where C_k is the

constant of integration and dependent upon the formation permeability k and    To exclude Ck, we substitute the values of variables at the borders of site wall dr, namely r = R_к and r = r_c, in equation (1.4) and obtain the following two equations:

when r = R_к, we will obtain the formation pressure, i.e. Р=Р_пл

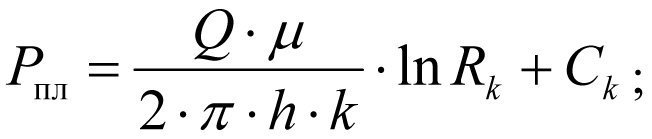     ;   (1.5)

and when r = r_c, we will obtain BHP, i.e. Р=Рз(k),

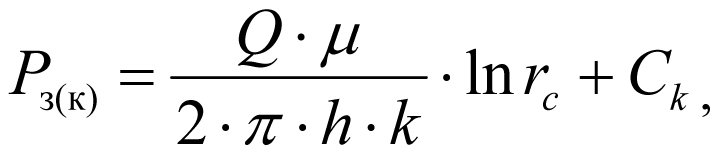   ,    (1.6)

where Рпл is the formation pressure and Р_з(к) is the pressure near the well wall (BHP) under the native formation permeability k.

Subtracting the equation (1.6) from equation (1.5) we find the pressure losses ΔР_k in the process of filtration of formation fluid into the well under the natural formation permeability k.

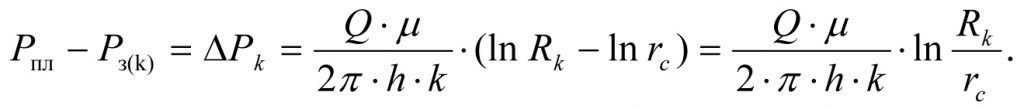 or

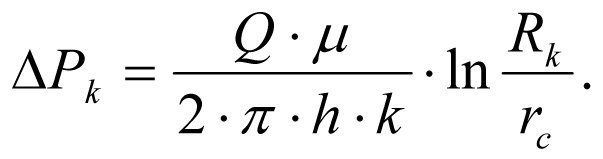      (1.7)                                        

Therefore, the formation pressure loss ΔР_k -in the process of fluid filtration in the borehole environment is in direct proportion to the natural logarithm of the ratio between the radius of external boundary of formation R_k and the well radius r_c and in inverse proportion to native formation permeability factor k.

It should be noted that the development of equation (1.7) is similar to that of the thermal conductivity equation of a cylindrical wall [4], and in the single-phase filtration theory, equation (1.7) is known as the Dupuis formula.

Equation (1.7) is a logarithmic curve equation, hence during fluid filtration through the formation to the well the pressure drop ΔР_k changes in accordance with the logarithmic law (see Fig. 1.1).

1.2. Development of the formula for calculation of BHP loss ΔР_s during fluid filtration in the borehole environment (in skin zone) of the real borehole

A. F. Van Everdingen and N. Hurst (1949) offered formula (1*) for calculation of the pressure loss in the borehole environment during fluid filtration into the well. [12].

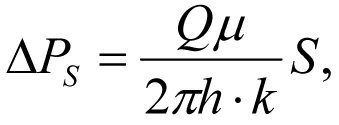  (1*)      

where ΔР_s are the additional losses of formation pressure during liquid filtration into the well caused by the impairment of formation permeability of a skin layer from k to ks; µ, which is the dynamic viscosity of the formation liquid Q; and S is the value of skin factor.

It should be noted, that analytical development of expression (1*) does not exist (and cannot exist!). Besides, in formula (1*) for the calculation of ΔР_s there were major mistakes [1,3, 11], where the physical laws of formation hydrodynamics were waived, the mathematical logic was ignored resulting in the abovementioned serious mistakes. In 1956, M.F. Hawkin, using a (1*) proposed formula to calculate skin factor S.  (2*),

which is currently known in educational and scientific books as Hawkins’ formula [13]. 

According to this formula, S may assume values from minus infinity to zero and from zero to plus infinity, i.e.

  ,

without belonging to the domain of definition, existence and practical application. It is known that if function tends to infinity, it has no any practical application. 

Formulas (1*) and (2*) are impractical in terms of defining ΔР_s, S and other basic parameters included in the system, and must be excluded from text books and tutorials on subsurface hydrodynamics. Parameters ΔР_s and S are of great importance and are included in formulas for all basic hydrodynamic parameters in the system of zonally heterogeneous formations. Thereby, this work gives four versions of development of the formula for calculation of ΔР_s  value and five versions to calculate the skin factor value S. 

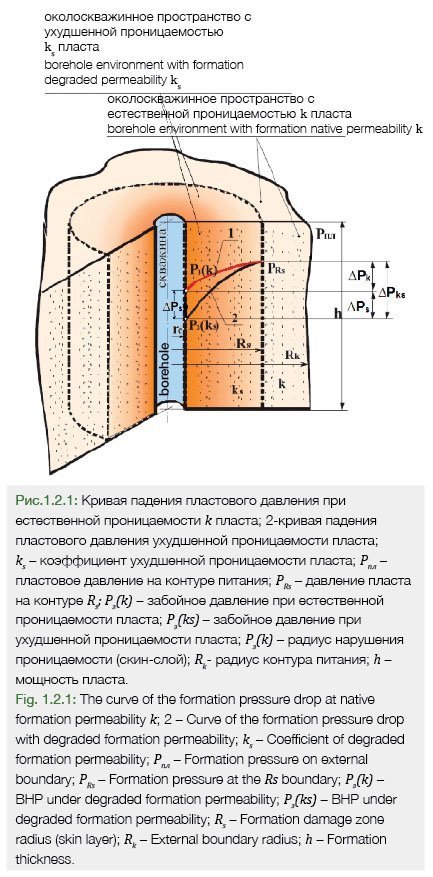
For further analysis, the logarithmic curve of formation pressure drop from Fig. 1.1 is transferred to Fig. 1.2 (curve 1).

Degradation of the permeability of the borehole environment from k to k_s by the ∆k value reduces the BHP from Р_з(k) to Р_з(ks) by the ∆Рs value (see Fig. 1.2) where Рз(k) is the BHP under the native formation permeability k (BHP of ideal well) and Рз(ks)  is the BHP under the degraded formation permeability, ks (BHP of real well). The formation pressure at the boundary R_s is equal to Р_Rs.  Curve 1 describes the formation pressure losses during fluid filtration in the borehole environment at its original permeability k, so equation (1.7) will look like follows (for ideal well).        

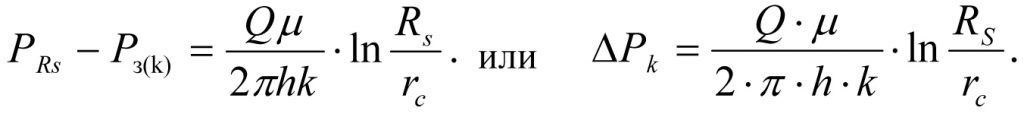  (1.8)

Curve 2 describes the formation pressure losses during fluid filtration in the borehole environment with degraded formation permeability k_s, so equation (1.8) will look like follows (for real well).       

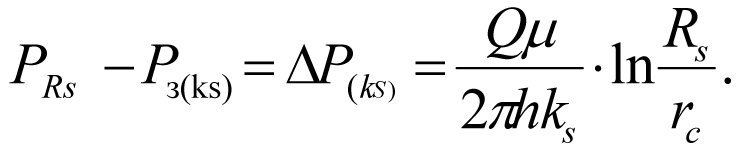 (1.9) 

BHP losses by ΔР_s value obtained through the difference between Р_з(к) and Р_з(кs) (see Fig. 1.2), is the result of the skin factor S, i.e

 .   (1.10)

The pressure drop ∆Р_(ks) in the skin layer gives (see Fig. 1.2 and formula (1.9))

  (1.11)

The BHP drop by the value of ΔРs is proportional to the skin factor S, i.e. ΔРs is an additional filtration resistance caused by the degradation of the formation permeability in real well from k to k_s, hence:      

 (1.12)

Using the equations (1.9) and (1.12) let us write down the formation BHP drop ΔРs for zonally heterogeneous formation as a result of disturbance of its permeability from k to k_s

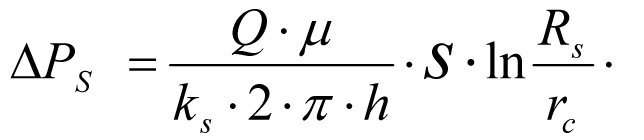 (1.13)              

Equation (1.13) was obtained by the author in 2003 and published in 2005 [7] and is the key equation for calculation of all hydrodynamic parameters of the real well zonally heterogeneous formation system.

1.2. Development of the formula for ∆P_s of zonally heterogeneous formation by taking the pressure loss within external boundary interval (R_k-R_s) and in skin layer (R_s-r_c) into account (see Fig 1.3).

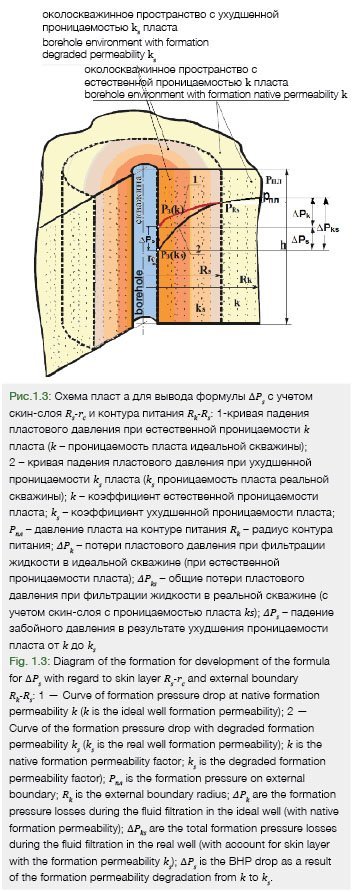
More compelling is deriving the equation for calculation of ∆P_s with account of pressure loss during plano-radial filtration of formation fluid in the zonally heterogeneous (by permeability) formation within the external boundary interval (R_k-R_s) at the formation permeability k and in the skin layer (R_s-r_c) with permeability k_s.

On the [R_k-R_s] section the permeability coefficient is equal to k, therefore we can use the formula (1.4), from which we find with r = R_k and r = R_s : when r = R_k we obtain the formation pressure Рпл:             

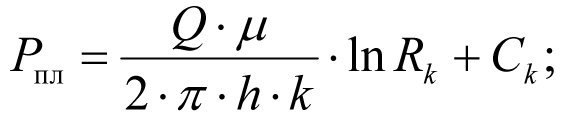    (1.17)                                                                               

and when r = R_s, we obtain the pressure on external boundary, so that R_s equal to РR_s,

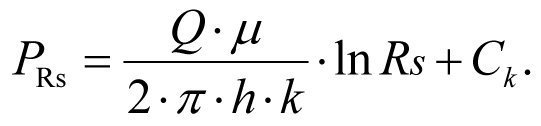    (1.18)

Subtracting the equation (1.18) from equation 1.17) we find the pressure losses at the section [R_k-R_s] with permeabilityk:                  

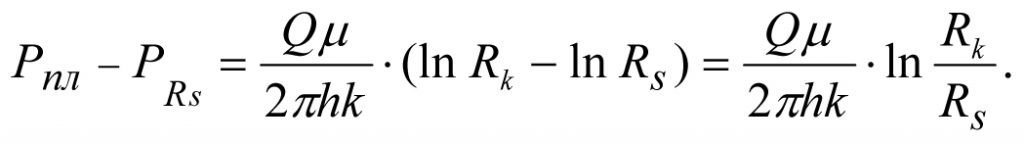  (1.19)   

On the [R_s-r_c] section permeability factor is equal to k_s, and

  .

Inserting in general formula (1.4) the values k_s, r = r_c и r = R_s instead of k with r = r_c, we obtain BHP

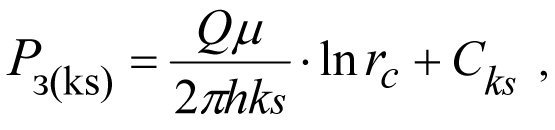   (1.20)

where   – is the integration constant related to permeability factor k_s. and with r = R_s we obtain the pressure on external boundary R_s,                   

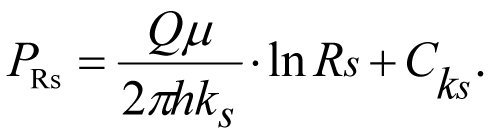  (1.21)

After subtracting the equation (1.20) from equation (1.21) we find pressure losses in the skin layer with permeability k_s 

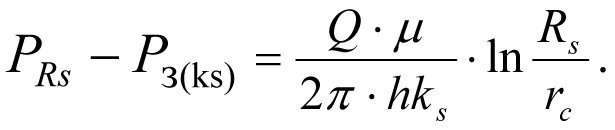 (1.22)                                             

Summing (1.19) and (1.22) we find the pressure losses in the formation zonally heterogeneous interval [R_к, r_c]: 

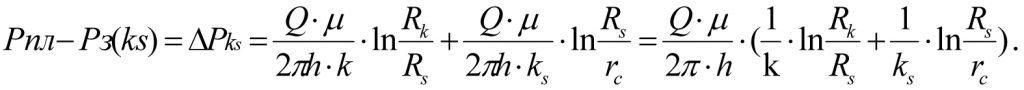  or

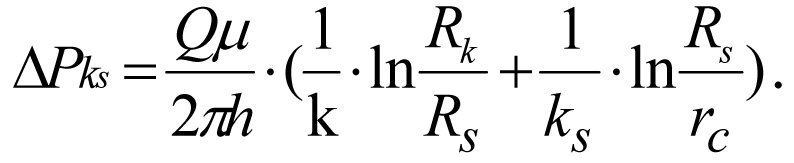 (1.23)                                                                                                                                         

The pressure loss in the borehole environment with native formation permeability k (Curve 1) will be equal to

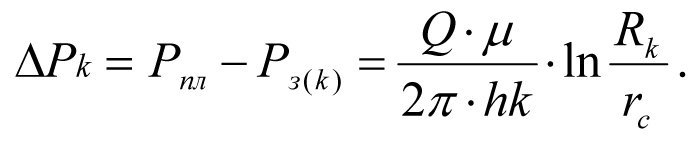 (1.24)

Deducting (1.24) from (1.23) we obtain the formula for calculation of BHP loss ∆Ps during fluid filtration in the zonally heterogeneous formation (see Fig.1.3).

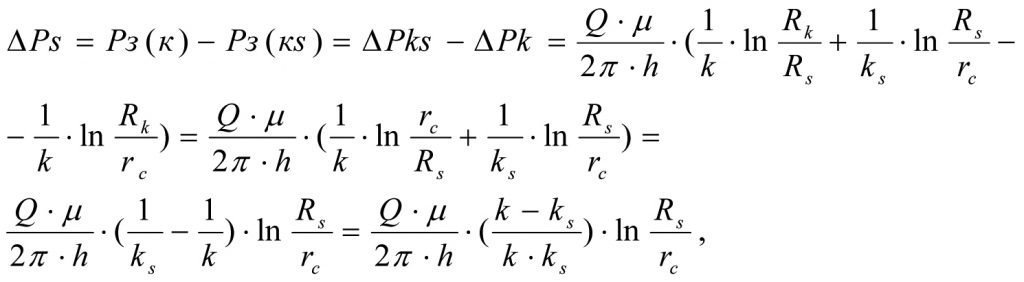or     

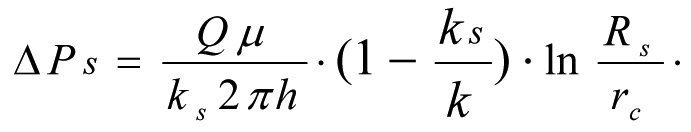  (1.25)

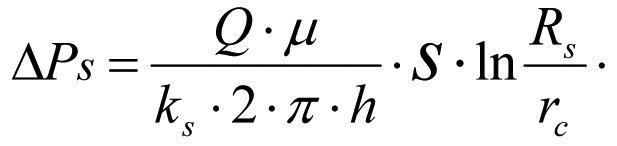  (1.26)

1.4. Development of the formula for calculation of ∆P_s for zonally heterogeneous formation under constant flow rate (Qж-const) (Fig.1.3)

The pressure loss in the borehole environment with formation native permeability k (Curve 1) will be equal to

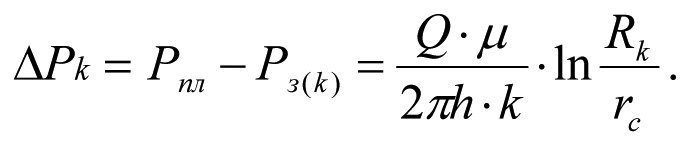  (1.27)            

In this case, the total pressure difference in the zonally heterogeneous formation will be:

 (1.28)

Pressure loss within the external boundary with permeability k will be:

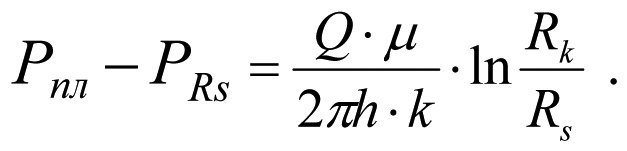 (1.29)

Pressure loss within the skin layer with permeability k_s will be equal to:

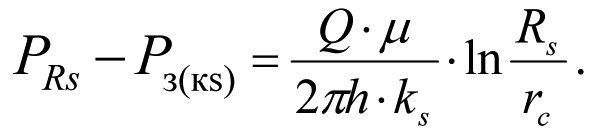 (1.30)

Inserting the values of (1.29) and (1.30) into (1.28) we obtain the pressure loss during plano-radial filtration of fluid in zonally heterogeneous formation by permeability.

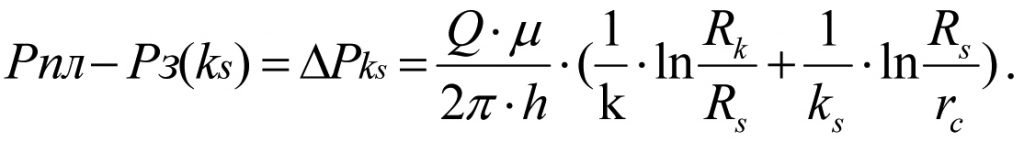   (1.31)

Deducting (1.27) from (1.31) we obtain additional pressure loss ∆P_s in skin layer as result of permeability degradation from k to ks (see Fig. 1.3).

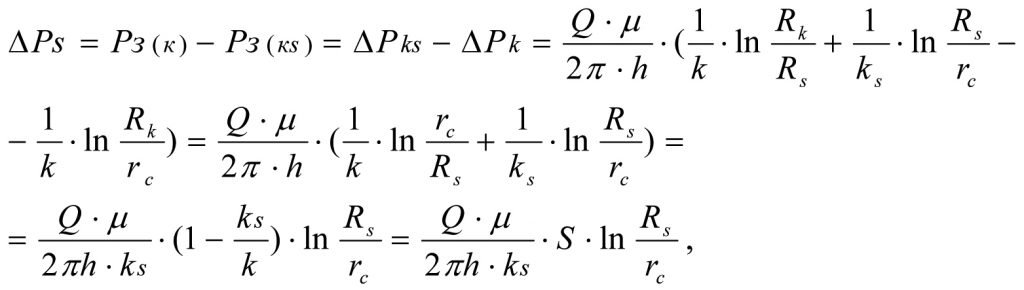or

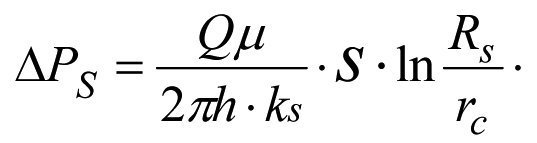 (1.32)                                       

Formulas (1.13), (1.26) and (1.32) obtained by different ways are identical.

2. Developing A formula to calculate skin-factor S      

A detailed formula for calculation of skin factor S is shown in works [1, 2, 8]. This formula is corroborated by the following indicator lines “production rate – pressure”, “production rate – level” and also through the values of the BHP and the potential production rate.

2.1 Development of skin factor S formula for zonally heterogeneous formations, i.e. with pressure loss within the borehole external boundary (R_k-R_s) and skin level (R_s-r_c) into account (see Fig. 1.3).     

The formation pressure drop during the fuel filtration to the bottomhole of the ideal well is equal to (1.24)

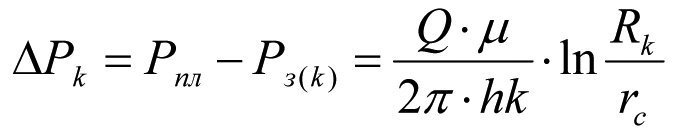
The pressure loss during plano-radial filtration of fluid in zonally heterogeneous formations by permeability will be (1.23)

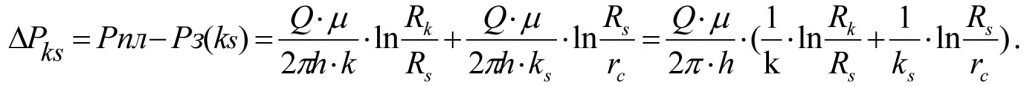
Deducting (1.24) from (1.23) we obtain the pressure loss ∆P_s in skin layer (see Fig. 1.3).

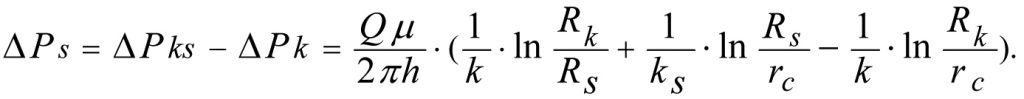  (2.1)

The BHP drop caused by disturbance of its permeability in skin layer from k to ks is equal to (1.13)                           

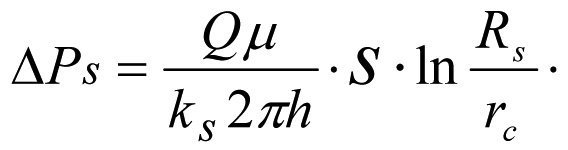  (2.2)

By setting the right sides of (1.28) and (1.29) equal we obtain the skin factor formula

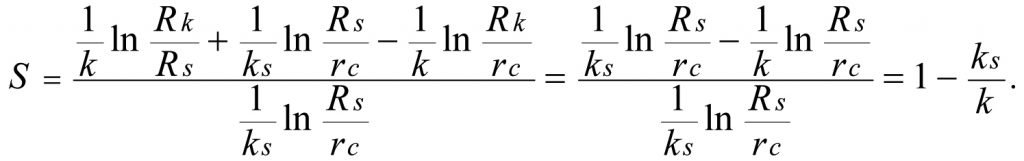
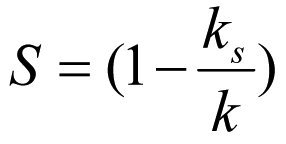  (2.3)

2.2. Developing the skin factor formula through indicator lines “production rate – pressure”   with Р_з=const and h_д=const (Fig. 2.1)

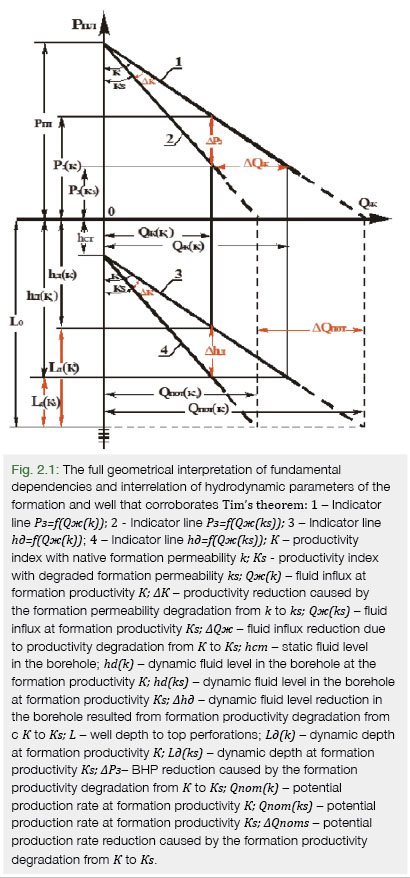
When the BMHs of the “ideal” and “real” well are equal, the volume influx (production rate) of fluid depends only upon the productivity index of the wells, whereas

Рз(кs)= Pз(к)= Рз;  Рпл-Рз(кs)=Рпл-Рз(к)=Рпл-Рз=ΔРconst.

Fluid influx to the bottomhole of the ideal well at the native formation productivity К will be equal to                       

Qж(к)=К . ΔΡ    (2.4)

Influx to the bottomhole of the real well at the formation degraded productivity К_s

Qж(ks) = Ks . ΔР.    (2.5)      

Fluid influx reduction ΔQ_ж into the well caused by the formation productivity decline from К to К_s will be equal to             

  (2.6)                                    

Because the fluid influx reduction is proportional to the skin factor, let us introduce the following term

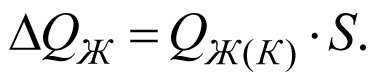 (2.7)        

Inserting (2.4) and (2.6) into (2.7), we obtain (2.8)

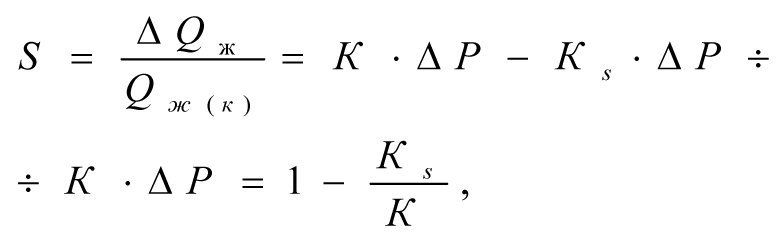  (2.8)

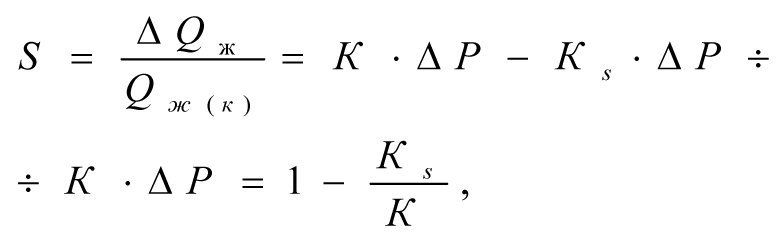
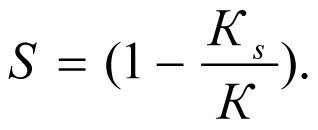  (2.9)

2.3.  Developing the skin factor S formula through indicator lines “production rate – level” at Q_ж const  (Fig. 2.1)

Fluid influx Q_ж to the bottomhole at the native formation productivity K will be equal to

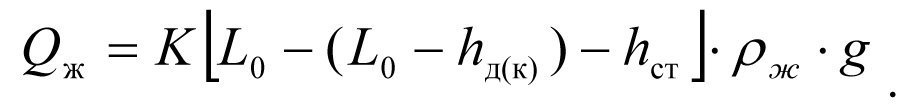 (2.10)

With permanent drainage, the productivity degradation from К_s to К_s causes the dynamic level to decrease from hд_(к) to hд_(кs), hence:

 (2.11)

Using (2.10) and (2.11), we determine dynamic levels at productivities К and К_s:

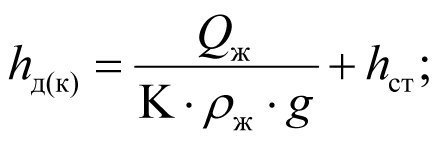 (2.12)              

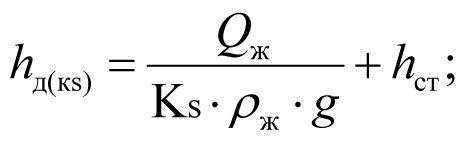 (2.13)

 The dynamic level drop Δh_д will be equal to

 (2.14)

Inserting the values of (2.12) and (2.13) into (2.14), we obtain

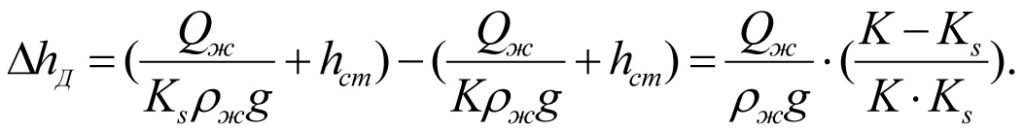  (2.15)

The dynamic level drop by the value of Δh_Д is proportional to the skin factor S, let us introduce the term                                           

  (2.16)       

Using equation (2.13), we write down

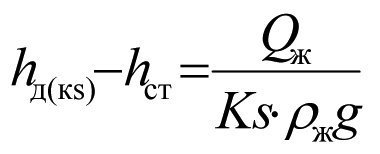 (2.17)

Inserting (2.15) and (2.17) into (2.16) gives

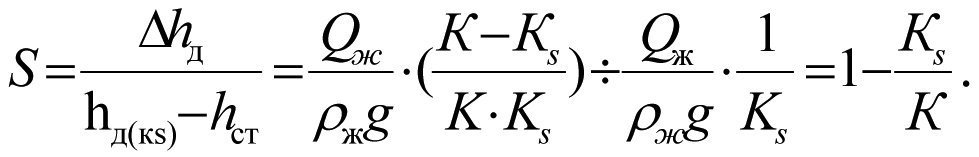 or

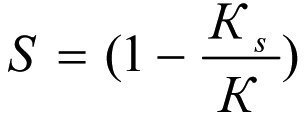   (2.18)

2.4. Developing the formula for skin factor S through the BHP value at Q_ж – const (Fig. 2.1)

Let us write down the fluid influx Q_ж equation at the productivity values К and К_s like follows                                                                                      

  (2.19)

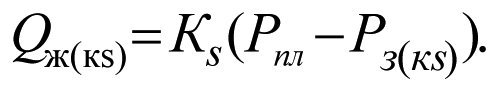 (2.20)

The BHP Р_з(к) at the natural formation productivity К is determined from formula (2.19):                         

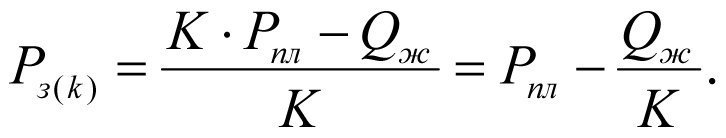 (2.21)

The BHP Р_з(кs) at the degraded formation productivity К_s, i.e., in the presence of a skin zone, is determined from formula (2.20)

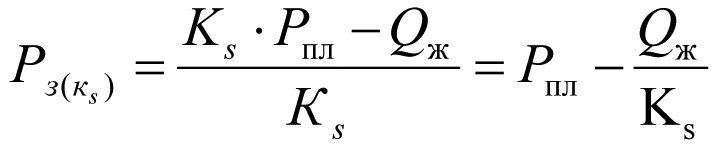  (2.22).   

At a constant drainage, the formation productivity decline from К to К_s causes the BHP to drop from Р_з(к) до Р_з(кs).

The BHP drop Δ_Рз will be equal to

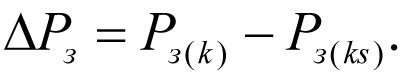 (2.23)                   

Inserting the values of Р_з(к) and Р_з(кs) into (2.23), we obtain

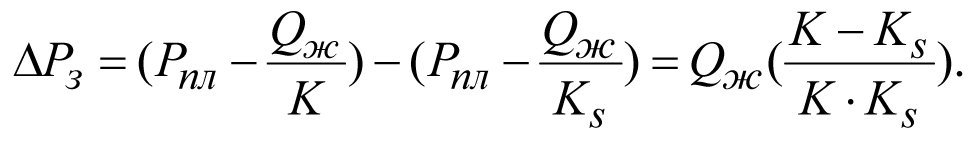  (2.24)

The BHP drop by the value of Δ_Рз is proportional to the skin factor S.

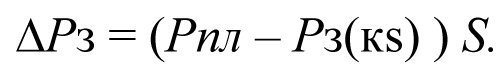 and 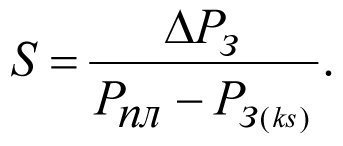  (2.25)

From formula (2.20) we write down

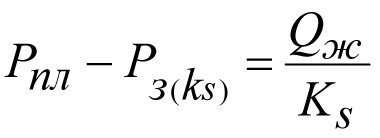 (2.26)

Inserting the values of (2.24) and (2.26) into (2.25), we obtain

or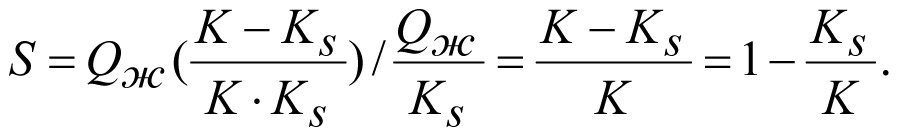      

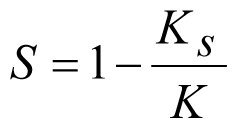  (2.27)

2.5. Developing the formula for skin factor S through the potential production rate (see Fig. 2.1)

The potential production rate of a well is a potential production that may be obtained at Р_з=0. The dynamic level of borehole fluid drops to the top perforations, i.e. h_д=L₀. The formation pressure remains unchanged, Р_пл – const.

According to the influx equation the potential production rate at productivity index К will be equal to

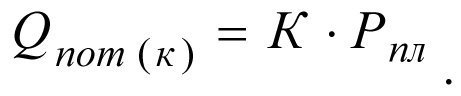   (2.28)

In the presence of a skin layer, the productivity index drops from К to К_s, so the potential  production rate will be          

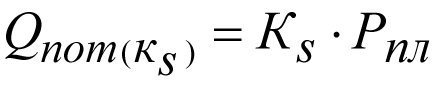 (2.29)

The reduction of potential production rate  ΔQ_пот resulted from degradation of formation productivity from К to К_s will be

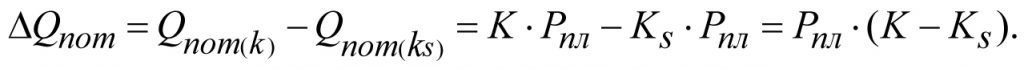
(2.30)

Reduction of the potential production rate by the ΔQ_пот value is proportional to the skin factor S,                                                            
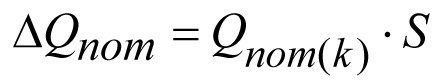 or 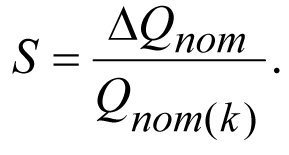   (2.31)

Inserting the value of (2.28) and (2.30) into (2.31), we obtain

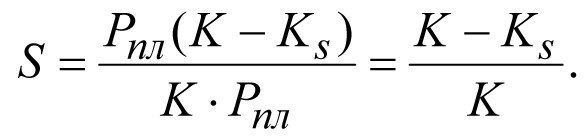
or 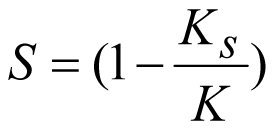  (2.32)

Formulas (2.3) and (2.9) for calculation of the skin factor value S derived with the use of permeability factors k and productivity К, are identical that allows to come to the following conclusions:

— The numerical value of the skin factor S shows the degradation share of the formation native permeability and is not logarithmical (logarithm under the s sign is a result of historical errors);    

— numerical value of the skin factor S is dimensionless;

— numerical value of the skin factor S has only a positive value (negative value of s is a result of historical fallacy) because the permeability factor k of the ideal formation always exceeds the permeability factor ks of the skin zone, i.e k >ks;

— definition domain of S (belonging), S ∈ (0,1];

— existence domain of S, 0<S≤1;

— If they following are equal – ks=k or К_s=К, the skin factor S is absent (when the formation is not disturbed);

— when ks=0 or К_s=0 the skin factor S assumes a maximum value, i.e. S=1 (the case of absolutely impermeable formations).

The skin factor is a complex parameter which integrally reflects all kinds of collector disturbance mechanisms affecting the degradation of the permeability and porosity of the productive formation borehole environment as well as the reduction of the formation water influx.

The skin factor has a huge negative impact at all stages of a hydrocarbon deposit from reservoir engineering up to well abandonment:

— at the stage of reservoir engineering, the skin factor is introduced in the form of design errors;

— at the stage of reservoir construction and development, the skin factor is provided in the form of committed design errors;

— at the production stage, the skin factor is implemented in the form of huge cost overruns and irreversible formation damage.

To be continued

References

1. Муфазалов Р.Ш.  Скин-фактор. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта.  Георесурсы. № 5. 2013. С. 34-48.

2. Муфазалов Р.Ш. Скин-фактор и его значение для оценки состояния околоскважинного пространства продуктивного пласта. // Научно-технический журнал «Технологии ТЭК» №3(34). 2007. С.36-42.

3. Муфазалов Р.Ш. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта при выводе формулы Скин-фактора. // Материалы международной научно-практической конференции «Инновационные технологии в геологии и разработке углеводородов». Казань: Изд-во НПО «Репер». 2009. С.303-310.

4. Михеев М. А. Основы теплопередачи: Учебник для вузов. –М.: Госэнергоиздат,     1949.-   396с.

5. Муфазалов Р.Ш. Скин-Фактор. Фундаментальные зависимости параметров пласта, скважины и оборудования. // Материалы международной научно-практической конференции «Актуальные вопросы разработки нефтегазовых месторождений на поздних стадиях». Уфа: Изд-во УГНТУ. 2010. С.80-93.

6. Муфазалов Р.Ш. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта и их последствия. Часть 1, 2, 3. // Труды 12 – Международного симпозиума «Энергоресурсоэффективность и энергосбережение». Казань: «Центр Оперативной Печати». 2011. С.409-464.

7. Муфазалов Р.Ш. Скин-фактор и его значение для оценки состояния околоскважинного пространства продуктивного пласта. Уфа: Изд-во УГНТУ. 2005. 44 с.

8. Mufazalov R.Sh. SKIN FACTOR and its importance for evaluating borehole environmental conditions for a productive formation. // «ROGTEC», Oil & Gas Magazine. Is. 19. Р. 18-36.

9. Муфазалов Р.Ш. Теорема Тима. Фундаментальные зависимости гидродинамических параметров пласта и скважины, и их взаимосвязь – основа инновационного проектирования процессов разработки нефтегазовых месторождений. // Материалы Международной научно-практической конференции «Моделирование геологического строения и процессов разработки – основа успешного освоения нефтегазовых месторождений». – Казань: Изд-во «Слово», 2018. с. 67 – 69.

10. Mufazalov R. Sh. Skin-Factor. Fundamental Relationships and interrelations Relationships, Conclusions and the Formula for the Key Hydrodynamic Parameters. // «ROGTEC», Oil & Gas Magazine. Is. 41. Р. 74-88.

11. Mufazalov R. Sh. Fundamentals of Subsurface Hydrodynamics and a Quantum-Mechanical View of the Reservoir Model. // «ROGTEC», Oil & Gas Magazine. Is. 55. Р. 42-57.

12. Van Everdingen A.F., and Hurst W., «The Application of the Laplace Transformation to Flow Problems in Reservoirs», Trans. AIME, Vol. 186, 1949, pp. 305–24.

13. Hawkins M. F. Jr., «A note on the skin effect», Trans. AIME, Vol. 207, 1956, pp. 356–57.

Author: R. S. Mufazalov, Paker Scientific and Production Firm, Oktyabrskiy, Republic of Bashkortosta