ЛУКОЙЛ: Мониторинг разработки месторождения с использованием статистических методов анализа на примере перфорационных работ

В условиях длительной разработки месторождения, с целью увеличения продуктивности скважин применяют различные геолого-технические мероприятия для интенсификации притока. Одни из них методов являются перфорационные работы (дострел не перфорированного ранее интервала и перестрел уже работающего). Особенностью данного метода является его невысокая стоимость, а прогнозирование эффекта может проводится по небольшому числу исходных параметров. Часто полученный эффект от мероприятия не соответствуют ожидаемому, в связи с чем возникает необходимость прогнозирования результатов с более высокой точностью.

В представленной работе в качестве объекта исследования выбран пласт БВ8 Повховского месторождения. Данный объект выбран в связи с достаточным для анализа объемом фактически проведенных дострелов: 1376 мероприятий.Выполнен поиск зависимостей между влияющими параметрами и эффективностью мероприятий для построения математических моделей с применением стандартного пакета «Анализ данных» MS Excel и методов Data Mining (регрессия нейронной сети, линейная регрессия), позволяющих находить скважины-кандидаты для определенных работ. Подход, используемый в работе, может быть распространен на другие эксплуатационные объекты и месторождения, а также на другие виды геолого-технических мероприятий.

Введение

В условиях длительной разработки место- рождения с целью увеличения продуктивности скважин проводят различные геолого- технические мероприятия (ГТМ) по интенсификации притока. Одними из них являются перфорационные работы (дострел не перфорированного ранее интервала и перестрел уже работающего). Особенностью данного метода является его невысокая стоимость, а эффект может прогнозироваться по небольшому числу исходных параметров. В настоящее время накоплен значительный объем информации по мероприятиям данного типа. Целью работы является поиск зависимостей между влияющими параметрами и эффективностью мероприятий для построения математических моделей, позволяющих находить скважины-кандидаты для определенного вида работ на примере объекта БВ8 Повховского месторождения. Данный объект выбран в связи с достаточным для анализа объемом фактически проведенных мероприятий: 1376 дострелов.

Повховское месторождение открыто в 1972 г., введено в разработку в 1978 г. Месторождение находится в Сургутском районе Ханты- Мансийского автономного округа Тюменской области, в 80 км от г. Когалыма. В разработке находятся объекты: БВ8, Ач и ЮВ1. Месторождение многопластовое со сложным геологическим строением. Нефтеносность установлена в отложениях мегионской, баженовской, васюганской и тюменской свит. По величине запасов месторождение относится к категории крупных. Наибольший объем за- пасов приходится на продуктивный пласт БВ8, который характеризуется самой высокой проницаемостью. Объект БВ8 является основным, определяющим добычу месторождения. Основная площадь объекта разрабатывается с 1978 г. В настоящее время отбор составляет 85,2 % начальных извлекаемых запасов (НИЗ) при обводненности продукции 89,5 %. Обработка собранной информации по фактически выполненным дострелам включала: – построение моделей для оценки прироста дебита жидкости и изменения обводненности с применением пакета «Анализ данных» в MS Excel; – построение моделей с использованием методов Data Mining (регрессия нейронной сети, линейная регрессия) в MS Azur MLS. На первом этапе исследования были проведены сбор и обработка геолого-промысловых и технологических данных по фактически проведенным дострелам. Общее число перфорационных работ составило 5810. Для анализа выбраны мероприятия, удовлетворяющие следующим критериям:

• перфорационные работы не являются первичными для конкретной скважины, но являются первичными для определенного прослоя (1653);

• в базу включены дострелы, осуществленные с 2000 г. (1256);

• дострелы проводились без гидроразрыва пласта (541);

• период простоя скважины перед проведением дострела не превышает 1 года (420);

• дострелы выполнены на добывающем фонде скважин (213);

• дострелы осуществлялись без проведения дополнительных мероприятий (195);

Регрессионные модели, полученнын в результате выполнения работы, легко реализуются и показывают достаточно высокие коэффициенты детерминации. Подход, используемый в работе, может быть распространен на другие эксплуатационные объекты и месторождения, а также на другие виды ГТМ

Исходя из формулы Дюпюи, основными параметрами, влияющими на дебит жидкости, являются: толщина, проницаемость пласта, депрессия, контур питания, вязкость и скин-фактор. Для построения математической модели оценки дебита жидкости приняты первые три параметра ввиду высокой точности их определения. В уравнение также добавлен параметр – максимальный дебит жидкости окружающих скважин, для оценки фактической продуктивности пласта. Для определения обводненности после проведения мероприятия приняты следующие параметры: величина текущих извлекаемых запасов нефти на 1 м толщины пласта – учитывает текущее насыщение пласта; обводненность до мероприятия – учитывает влияние уже подключенных прослоев в скважине на значение обводненности после мероприятия; прирост дебита жидкости после мероприятия – учитывает взаимовлияние фаз воды и нефти. В первую очередь в данной работе рассматривается построение моделей методом линейной регрессии с использованием встроенного пакета «Анализ данных» в MS Excel. Суть регресссии заключается в определении степени влияния каждого из предполагаемых влияющих параметров X1, … , Xn на зависимую переменную Y. Далее находят коэффициенты регрессии Ki для наилучшего представления дебита жидкости и обводненности после проведения дострела [1–3]

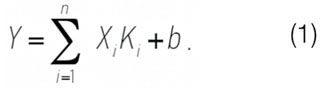
Построение моделей для оценки прироста дебита жидкости и изменения обводненности с применением пакета «Анализ Данных» В MS Excel

На первом этапе строилась модель для прироста жидкости после дострелов. Коэффициенты регрессии, значения стандартных ошибок, критерия Стьюдента t, P-значения представлены в табл. 1. Формула для определения прироста дебита жидкости Yq после проведения мероприятия в модели линейной регрессии имеет следующий вид:

Yq = -0,1965X1 + 0,0936X2 + 0,1861X3 +  0,0013X4 — 5,5673. (1)

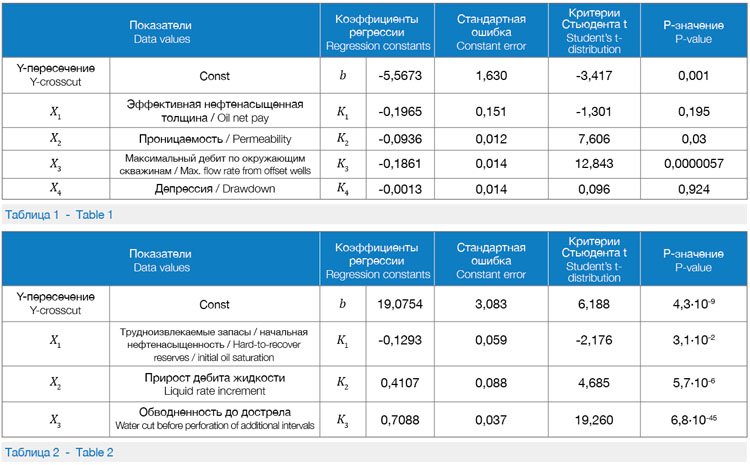
Сопоставление расчетного дебита жидкости с фактическим после дострела показывает высокую сходимость полученных результатов, коэффициент детерминации R2 = 0,712 (рис. 1). По нефтенасыщенной толщине и депрессии Pзначение составляет более 0,05, что согласно правилам описательной статистики означает слабое влияние фактора на результирующий параметр или отсутствие влияния. Полученные результаты можно объяснить следующим образом. Во-первых, возникает неопределенность в выборе версии интерпретации геологофизических параметров. Например, в скв. 2598 по актуальной версии «Переинтерпретация_2011 год» выделен коллектор с нефтенасыщенной толщиной, равной 1,5 м, а по версии «ООО_ЦСРМнефть_2011 год» соответствующий параметр составляет 12,1 м, при этом результаты потокометрии согласуются со второй версией интерпретации. Во-вторых, пластовое давление снимается с карты изобар, при этом карты строятся с периодичностью один раз в квартал по некоторому числу значений, полученных непосредственно в скважинах, остальная часть значений рассчитывается.

Забойное давление в большинстве случаев пересчитывается через динамический уровень, что также снижает качество исходной информации. Далее проводилось построение модели для определения обводненности после проведения дострелов. Коэффициенты регрессии, значения стандартных ошибок, критерия Стьюдента t, P-значения представлены в табл. 2. Формула для определения обводненности Yf после проведения мероприятия в модели линейной регрессии выглядит следующим образом:

Yf = -0,1293X1 + 0,4107X2 + 0,7088X3 + 19,0754. (2)

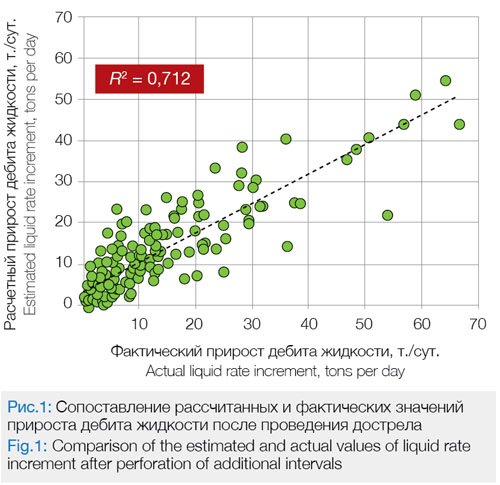
Сопоставление расчетной и фактической обводненности после проведения дострела показывает высокую сходимость полученных результатов, R2 = 0,8185 (рис. 2).

Data Mining – собирательное название, используемое для обозначения совокупности методов обнаружения ранее неизвестных, нетривиальных, практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности [4]. Data Mining развивалась на стыке таких дисциплин, как статистика, теория информации, машинное обучение, поэтому большинство алгоритмов было разработано на основе различных методов из этих дисциплин. Data Mining включает: теорию баз данных, распознавание образов, описательную статистику, машинное обучение, визуализацию, алгоритмизацию, искусственный интеллект. При этом существует множество программ для реализации задач Data Mining, такие как R-Studio, Microsoft Azure MLS, Orange и др.

Построение моделей с применением программного продукта Microsoft Azure MLS

В представленной работе рассмотрены два метода: метод линейной регрессии и метод регрессии нейронной сети, реализованные в программном продукте Microsoft Azure MLS (рис. 3). Данный софт достаточно прост в понимании, бесплатный, имеет встроенные модули, в которых реализованы различные алгоритмы, при этом соблюдается конфиденциальность загружаемых данных в связи с их обезличенностью. Создание эксперимента в студии машинного обучения включает следующие шаги: – передача набора данных в виде CSV-файла (табличные данные в текстовом формате) в студию машинного обучения; – создание эксперимента и использование модуля Select Columns in Dataset (выбор столбцов в наборе данных) для выбора тех же признаков данных, что используются в MS Excel;
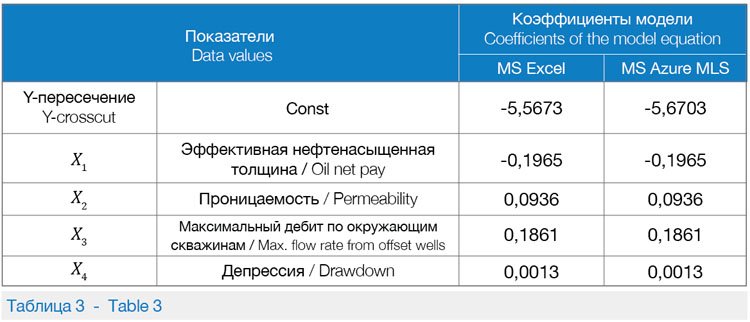
• использование модуля Split Data (разделение данных) в режиме относительного выражения для разделения данных на точно такие же наборы данных для обучения, как в MS Excel. При использовании модуля «Линейная регрессия» в студии машинного обучения доступны два метода: метод градиентного спуска в режиме онлайн (для крупномасштабных проблем); метод наименьших квадратов (наиболее распространенный метод линейной регрессии). Это оптимальный выбор для небольшого объема данных. В табл. 3 представлено сравнение коэффициентов, полученных в моделях MS Excel и MS Azure MLS для расчета прироста дебита жидкости. Видно, что полученные модели имеют схожие показатели.

Далее в работе был рассмотрен метод Data Mining – «Регрессия нейронной сети» (рис. 4). Алгоритм нейронной сети (Microsoft) полезен при анализе большого объема данных. В службах SQL Server Analysis Services алгоритм нейронной сети (Microsoft) сочетает каждое возможное состояние входного показателя с каждым возможным состоянием прогнозируемого показателя и использует обучающие данные для вычисления вероятностей.

Далее эти вероятности можно применять для прогнозирования рассматриваемого параметра на основе входных данных. В модели интеллектуального анализа данных, которая создается при помощи алгоритма нейронной сети Microsoft, может содержаться несколько сетей. Их число определяется числом столбцов, используемых для входа. Алгоритм создает сеть, состоящую из двух или трех слоев нейронов. К таким слоями относятся входной, необязательный скрытый и выходной слои. Модель нейронной сети должна содержать ключевой столбец, один или несколько входных и прогнозируемых столбцов.

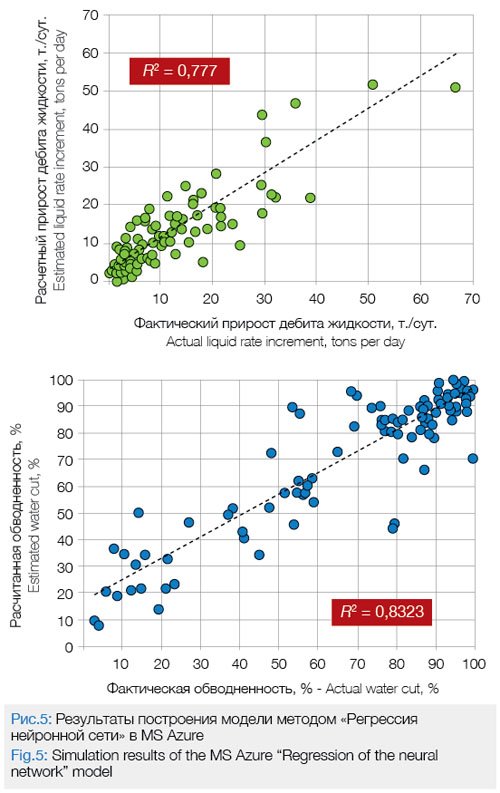
На рис. 5 приведены результаты расчета прироста дебита жидкости и изменения обводненности, с помощью моделей, построенных в MS Azure MLS методом «Регрессия нейронной сети». Из рис. 1, 2 и 5 видно, что модель, построенная в MS Azure MLS методом «Регрессия нейронной сети», характеризуется несколько лучшей сходимостью с фактическими показателями.

Заключение

Внедрение Big Data технологий в процесс разработки месторождений является неоспоримо перспективным направлением. Выполненная работа указывает на возможность применения методов Data Mining для анализа исходных данных по фактически проведенным операциям дострелов, а также для прогноза эффективности планируемых. Регрессионные модели, полученные в результате выполнения работы, легко реализуются и показывают достаточно высокие коэффициенты детерминации. Подход, используемый в работе, может быть распространен на другие эксплуатационные объекты и месторождения, а также на другие виды ГТМ.

Список литературы

1. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1991. – 400 с.

2. Макарова Н.В., Трофимец В.Я. Статистика в Excel. – М.: Финансы и статистика, 2002. – 368 с.

3. Савельев В. Статистика и котики. – М.: Издательские решения, 2017. – 126 с.

4. http://pandia.ru/text/78/271/8297.php

Авторы статьи:

А.А. Анкудинов, к.т.н.,

Н.С. Полякова,

Ю.Е. Радевич

Филиал ООО «ЛУКОЙЛ-Инжиниринг» «КогалымНИПИнефть» в г. Тюмени

Материал любезно предоставлен компанией ПАО «Газпром нефть» и журналом «PROнефть»