Модель для экспресс оценок дизайна ГРП с использованием приближенного аналитического решения

В работе приводится аналитическое решение модели Pseudo3D для гидроразрыва пласта в упрощённой геомеханической постановке. Задача решается в безразмерных параметрах для обеспечения универсальности решения. Строятся графики безразмерной длины от высоты, а также график Aspect ratio трещины для разных.

Полученное решение позволяет быстро находить геометрию трещины при развитии ГРП, а также оценить нужный объём закачки жидкости ГРП для достижения нужной длины трещины, в том числе и при гибридном ГРП с несколькими жидкостями.

Введение

Гидроразрыв пласта (ГРП) – основной метод интенсификации нефтедобычи в традиционных и нетрадиционных коллекторах. Планирование, сопровождение и оптимизация операций ГРП осуществляется с использованием специализированных программных пакетов. Например, MFrac, FracPro, FracCADE, Mangrove, которые либо продаются добывающим и нефтесервисным компаниям, либо являются внутренними разработками нефтесервисных компаний, и расчеты в них предоставляются только как часть сервисных услуг. Все применяемые симуляторы ГРП на активах компании ПАО «Газпром нефть» является импортными, приобретение лицензий (услуг) которых в связи с санкционными ограничениями значительно затруднено. Поэтому, разработка собственных подходов математического моделирования дизайна ГРП является одной из приоритетных задач в отрасли в рамках стратегии импортозамещения.

Основные аналитические решения (PKN, KGD, Radial) в теории ГРП получены в 50-70х годах двадцатого века. Из этих трех моделей наиболее адекватной для месторождений западной Сибири является модель PKN [1,2]. Однако, даже она не учитывает строение геологического разреза. Для учета этого стали разрабатываться численные модели такие, как Pseudo3D, Planar3D и Full3D, задействующие значительные вычислительные ресурсы. В данной же работе делает акцент на получении прокси и аналитического решения в Pseudo3D постановке.

Положения Pseudo-3D модели

Псевдотрехмерная модель [3,4] (см. рис 1) является по сути расширением модели PKN и строится на следующих предположениях:

1) Трещина растёт в плоскости, перпендикулярной минимальному горному напряжению, которое на больших глубинах имеет горизонтальное направление. Трещина растёт симметрично вправо и влево, а потому во многих симуляторах рисуется только одно крыло трещины. В нашей модели также имеется симметрия по вертикали

2) В моделях, описывающих трещину ГРП, вводится так называемое чистое давление p=p_f— σ₀, где p_f – полное давление флюида, а σ₀ – горное давление в коллекторе. На краю трещины полудлины L раскрытие w=0, а значит из уравнений линейной механики хрупкого разрушения p(L)=0. Сама граница трещины определяется двумя функциями L(t) и h(x,t). В представленной ниже формулировке эти функция заменены на L(h₀) и h(x, h₀) т.к. в нашей постановке для любого времени t соответствует свое значение h₀ – высоты трещины в центре, а значит и само время представимо как t(h₀).

3) Вертикальный поток жидкости считается пренебрежимым по сравнению с горизонтальным. Это выполняется, когда основной рост трещины идет по горизонтали. В каждом вертикальном сечении выписывается закон сохранения массы, горизонтальный поток усредняется по вертикали.

4) Раскрытие трещины в каждом профиле определяются условиями плоской деформации.
Это приближение следует из основного предположения h≪ L. Однако на кончике трещины это приближение все равно не выполняется.

5) Утечки в пласт рассчитываются по формуле Картера, в предположении одномерного течения около контура трещины.

Математическая постановка

Из плоской теории упругости [5] следует формула для профиля трещины высоты h с продуктивным слоем толщины H, контрастом напряжений ∆σ и трещинностойкостью соседних слоев K_I, модулем Юнга E и коэффициентом Пуассона ν:

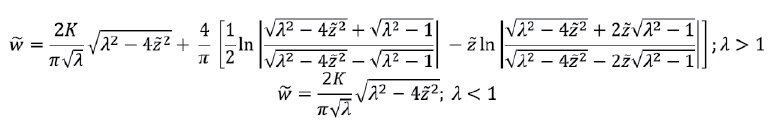
Здесь введены безразмерные параметры [6]:

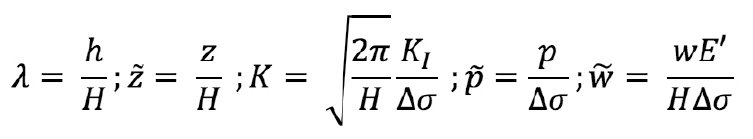
Здесь E’= 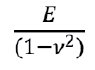       – модуль плоской деформации.

В безразмерном виде профиль трещины зависит только от безразмерной трещинностойкости K, которая для пластовых условий, как правило, не велика, и слабо влияет на раскрытие, и безразмерной высоты λ.

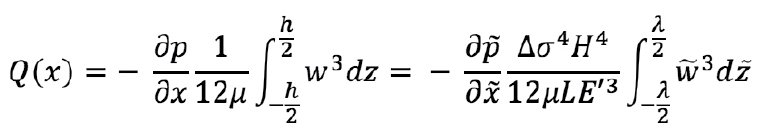
В той же манере выписывается уравнения Пуазейля для одномерного потока в трещине:

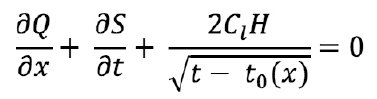
Основным уравнением развития трещины является закон сохранения массы  для одномерного течения:

где C_l – коэффициент утечек по Картеру, а S – площадь сечения вертикального профиля трещины.

Построение прокси моделей

Основная идея при построении прокси моделей состоит в отказе от численного решения путем построения разностных схем, как традиционном подходе Cell-based Pseudo3D [6]. За место этого предлагается использовать известные аналитические решения и проводить их сшивку. Например, в работе [7] предлагается для нахождения профиля ширины по высоте использовать точное аналитическое решение, для нахождения высоты — критерий Ирвина, для нахождения длины – решение PKN, а сшивку проводить по чистому давлению в отличии от предшествующих работ, например [8], где для нахождения чистого давления использовалось  некорректное приближение, а сшивка проводилась по значению высоты.

Получение аналитического решения

Получение приближенного аналитического решения стало возможным благодаря выделению новых безразмерных параметров отсутствующих в [6], а именно:

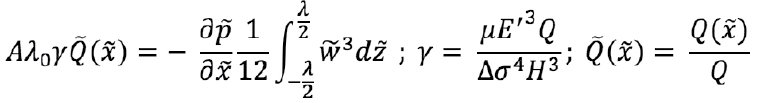
Здесь  A(h₀)= 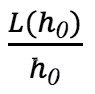  – «половинный» aspect ratio

трещины, а γ= 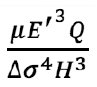   – малый параметр задачи, разложение по которому и позволяет нам получить новое аналитическое решение для задачи.

Физический смысл параметра γ заключается в отношение толщины пласта к характерной достижимой длине трещины. Чем меньше γ, тем больше получается длина трещины.

Для дальнейшего решения задачи выписывается безразмерная проницаемость трещины,

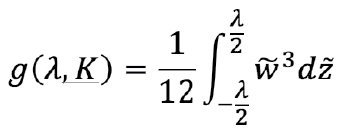
Для выделения безразмерных параметров выделяется обезразмеренное время:

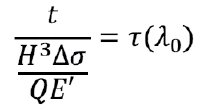
И получается следующее уравнение:

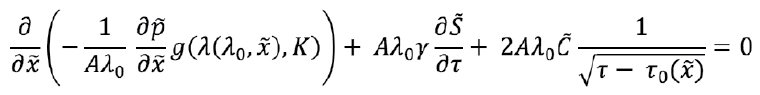
Оно дополняется граничным условием на поток в правую половину в начале трещины:

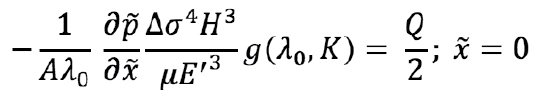
Или же:

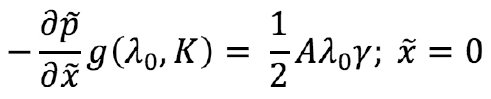
Здесь выделен безразмерный параметр утечек, который для большинства трещин является малым. Стоит отметить, что это параметр влияния утечек на форму, параметр «мгновенных» утечек. «Интегральный» параметр утечек как правило больше на несколько порядков. Этот параметр характеризует именно эффективность жидкости и итоговый объем трещины, но не её форму.

Аналитическое решение получается, если отбросить все члены в уравнении с малыми параметрами. Тогда, с учётом граничного условия, получается уравнение:

Которое означает, что поток жидкости вдоль трещины постоянен, то есть оттоки по вертикали пренебрежимо малы. Это и есть основное положение модели Pseudo3D.

Интегрируя уравнение по частям, получаем соотношение в квадратурах:

Где G(λ₀,K) – универсальная функция, характеризующая достигаемую обезразмеренную длину трещины при данной высоте, и имеет универсальный характер.

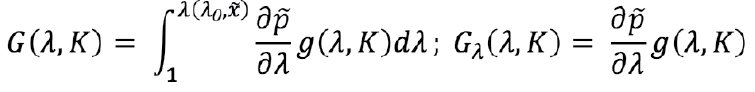
Её графики для разных значений параметра Kϵ(0,1) представлены ниже:

Полудлина трещины L находится по формуле:

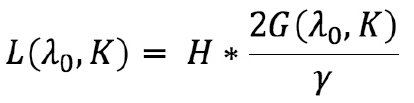
Здесь видно, что выделенный нами безразмерный параметр γ является единственным параметром, на который влияет дизайн ГРП, и который может влиять на длину трещины.

Данные решения без труда обобщаются и на гели ГРП степенной реологии по той же схеме. Данное приближённое решение постоянного потока позволяет не только получать форму трещины для какого-то одного геля ГРП, но и для трещины, созданной разными гелями ГРП, применёнными поочерёдно. Пример расчета для гибридного ГРП изображен на рис. 3.

Выводы

В работе обозначены основные подходы моделирования ГРП в Pseudo3D постановке. Основным преимуществом прокси и приближенного аналитического решения является отсутствие необходимости построения численного решения нелинейного уравнения 2ого порядка.

Также стоит отметить, что аналитическое решение выполнено в безразмерных переменных и зависит от трех безразмерных параметров, что позволяет определить степень влияния литологии пласта и реологии жидкости на достижимые значения геометрии трещины ГРП. Также, отличительной особенностью данного решения является принципиальная возможность моделировать гибридный ГРП.

Литература

[1] T.K. Perkins and L.R. Kern. Widths of hydraulic fractures. J. Pet. Tech., Trans. AIME,

222:937–949, 1961.

[2] R.P. Nordgren. Propagation of vertical hydraulic fractures. J. Pet. Tech., 253:306–314, 1972. (SPE 3009).

[3] A. Settari and M. P. Cleary. Development and testing of a pseudo-three-dimensional model of hydraulic fracture geometry (p3dh). In Proc. 6th SPE Symposium on Reservoir Simulation of

[4] B. R. Meyer. Design formulae for 2d and 3-d vertical hydraulic fractures: Model comparison

and parametric studies. In Proc. Unconventional Gas Technology Symposium, pages 391–408. SPE 15240, 1986.

[5] N.I. Muschelehvili. Some basic problems of the mathematical theory of elasticity. P. Noordhoff, Groningen, The Netherlands,1953.

[6] J.I. Adachi, E. Detournay, A.P. Pierce. An Analysis of the Classical Pseudo-3D Model for Hydraulic Fracture with Equilibrium Height Growth across Stress Barriers, Int. J. of Rock Mechanics & Mining Sciences, Volume 47, Issue 4: 625–639, June 2010.

[7] G.V. Paderin. Modified Approach to Incorporating Hydraulic Fracture Width Profile in Unified Fracture Design Model, SPE Russian Petroleum Technology Conference, 2016, (SPE 182034)

[8] M.J. Economides, Olygney R.E, Valko P.P. Unified Fracture Design, Texas:Orsa Press Alvin

Авторы статьи:  Шель Е.В., Падерин Г.В. Научно-Технический Центр «Газпром нефти»

(ООО «Газпромнефть НТЦ»).

Материал любезно предоставлен компанией ПАО «Газпром нефть» и журналом «PROнефть».

Bibliography

[1] T.K. Perkins and L.R. Kern. Widths of hydraulic fractures. J. Pet. Tech., Trans. AIME,

222:937–949, 1961.

[2] R.P. Nordgren. Propagation of vertical hydraulic fractures. J. Pet. Tech., 253:306–314, 1972.

(SPE 3009).

[3] A. Settari and M. P. Cleary. Development and testing of a pseudo-three-dimensional model of hydraulic fracture geometry (p3dh). In Proc. 6th SPE Symposium on Reservoir Simulation of

[4] B. R. Meyer. Design formulae for 2d and 3-d vertical hydraulic fractures: Model comparison and parametric studies. In Proc. Unconventional Gas Technology Symposium, pages 391–408. SPE 15240, 1986.

[5] N.I. Muschelehvili. Some basic problems of the mathematical theory of elasticity. P. Noordhoff, Groningen, The Netherlands,1953.

[6] J.I. Adachi, E. Detournay, A.P. Pierce. An Analysis of the Classical Pseudo-3D Model for Hydraulic Fracture with Equilibrium Height Growth across Stress Barriers, Int. J. of Rock Mechanics & Mining Sciences, Volume 47, Issue 4: 625–639, June 2010.

[7] G.V. Paderin. Modified Approach to Incorporating Hydraulic Fracture Width Profile in Unified Fracture Design Model, SPE Russian Petroleum Technology Conference, 2016, (SPE 182034)

[8] M.J. Economides, Olygney R.E, Valko P.P. Unified Fracture Design, Texas:Orsa Press Alvin

Authors of the article:  Shel Egor Vladimirovich, Paderin Grigory Vladimirovich, LLC Gazpromneft Science & Technology Center.

Published with thanks to Gazprom Neft & PROneft Magazine

Шель Е.В., Падерин Г.В.
(ООО «Газпромнефть НТЦ»)