Фундаментальные основы подземной гидродинамики и квантомеханический взгляд на модель пласта

1. Теорема Тима. Фундаментальные зависимости базовых гидродинамических параметров пласта и скважины, и их взаимосвязь – основа новой парадигмы подземной гидродинамики

Система «Продуктивный пласт – скважина — насосное (лифтовое) оборудование» — единая, неразделимая гидродинамическая система, взаимосвязанная фундаментальными зависимостями, отражающими единство и взаимосвязь всех гидродинамических параметров этой системы [4]. Околоскважинное пространство продуктивного пласта – особая высокоактивная и энергодинамически нестабильная зона. В процессе первичного вскрытия продуктивного  горизонта бурением, заканчивания скважины (вторичного вскрытия) и ее эксплуатации нарушаются природное энергомеханическое и электродинамическое равновесия продуктивного пласта. В околоскважинном пространстве происходят гидротермодинамические, физико-механические изменения характеристики породы, свойства пластовой жидкости. Совершаются физико-химические, химико-биологические превращения. Происходит нарушение электромагнитодинамического равновесия пласта и в связи с этим в капиллярах и трещинах околоскважинного пространства образуются удерживающие водородные связи в углеводородных системах и происходит перераспределение энергии связи, определяемой силами Ван-дер-Ваальса и силовых полей взаимодействия двойного электрического слоя (ДЭС). Все эти технологические процессы и далеко не полностью указанные факторы существенно влияют на физико-реологические параметры пластовой жидкости, нарушают проницаемость и пористость околоскважинного пространства, образуя, так называемую, неоднородную по проницаемости и пористости скин-зону и приводят кратному снижению притока жидкости в скважину.

Van Everdingen A. F. и Hurst N. (1949) предложили формулу (1) для расчета потери давления в околоскважинном пространстве при фильтрации жидкости в скважину [1].

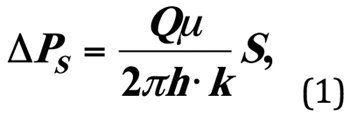
где ΔРs — дополнительные потери пластового давления при фильтрации жидкости к забою скважины из-за ухудшения проницаемости пласта в скин-слое от k до ks; µ — динамическая взякость пластовой жидкости Q; S — значение скин-фактора. Параметр ΔРs имеет важное значение и входит при выводе формул всех базовых гидродинамических параметров зонально-неоднородного пласта.

Следует отметить, что аналитический вывод выражения (1) не существует, кроме того, допущены следующие грубые ошибки:

• во-первых, по законам гидродинамики нефтяного пласта при фильтрации жидкости, значение ΔРs имеет логарифмическую природу, т.е. ΔРs изменяется  по логарифмической кривой, а в формуле (1) это не учтено. Эта серьезная ошибка внесла в значение S неопределенность и ± ∞;

• во-вторых, потери давления ΔРs зависит от величины радиуса (толщины) скин-слоя Rs, а в формуле (1) не учтена толщина скин-слоя Rs. Это противоречит законам гидродинамики пласта и существенно искажает реальное значение S;

• в-третьих, при определении ΔРs не учтен коэффициент проницаемости ks скин-слоя, т.к. ΔРs  — дополнительные фильтрационные потери в скин-зоне с коэффициентом проницаемости ks, поэтому значение коэффициента ks должно быть учтено. Эта грубая ошибка привела к полному искажению значения S.

Таким образом, в формуле (1), предложенной V.Everdingen A.F.и Hurst N.(1949) для определения ΔРs не соблюдены физические законы гидродинамики пласта, нарушена математическая логика и допущены указанные серьезные ошибки. Hawkin M.F.(1956), используя (1), предложил для расчета S формулу:

(2), вошедшую в учебную и научную литературу, как Hawkins’ formula [2].

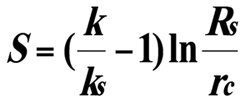
Согласно этой формуле, S может принимать значения  от минус бесконечности до нуля и от нуля до плюс бесконечности т.е.,
без принадлежности области определения, существования и практического использования. Известно, если функция стремится к бесконечности, она практического применения не имеет.   

Подземная гидродинамика как самостоятельная нефтяная  наука, основанная и сформированная отечественными учеными Н.Е. Жуковским, Н.Н. Павловским, Л.С. Лейбензоным, С.А. Христиановичем, В.Н. Щелкачевым и др., а также зарубежными учеными M. Muskat, Van Everdingen A.F.& Hurst N. и Hawkins M.F. к 50 годам ХХ века, казалось, полностью завершена, и проведены последние завершающие штрихи этой фундаментальной науки. Завершена в том смысле, что выявлены основные законы гидродинамики фильтрации пластовой жидкости, которым подчиняются глубинные процессы, происходящие в нефтегазовом пласте, написаны соответствующие уравнения и их решения. Сомневаться в надежности известных нам принципов этой науки не было оснований. Всякая динамично развивающаяся наука формулирует и определяет не только основные принципы, на которых она строится, но и должны быть определены основные направления и границы применимости этих принципов.     

Каких бы теоретических и технологических успехов не достигла современная наука в области гидродинамики пласта, она далека от совершенства и к концу 50-х годов практически полностью исчерпала свой потенциал и не создала ни одной фундаментальной теории, более того,  сформировалась ошибочная концепция по базовым направлениям.

Горечь удивления вызывает та реальность, что более полувека, начиная со второй половины ХХ го столетия, патриархи Российской и зарубежной нефтяной науки были уверены в непогрешимости формулы (Van Everdingen & Hurst, 1949) для определения ΔРs, скин-фактора S (Hawkins, 1956),  а также формулы для определения притока Qs к забою реальной скважины, несмотря на явные ошибки и спорные вопросы вокруг этих формул, составленных с грубыми нарушениями законов подземной гидродинамики.     

Негативные последствия этих ошибок и заблуждений нашли отражения в теории и практике основных положений ГДИС, ТИС и ГИС, но главные губительные последствия в том, что со второй половины прошлого столетия эти формулы без выводов и доказательств были включены во все учебники,  учебные пособия и методические руководства соответствующего профиля вузов и курсов повышения квалификации.     

Современная подземная гидродинамика больна изнутри. Основные причины болезни, ее  живучести и устойчивости – глубокий застой научных идей в сочетании с догматическим подходом к формированию и решению фундаментальных научных проблем, и консерватизмом научного мышления. Исследовательские работы в области подземной гидродинамики с тех времен и по настоящее время свелись к разработке полуэмпирических подгоночных теорий, имеющих предварительный характер ошибочных концепций. Пример тому, что по сей день оставались открытыми и дискуссионными наиболее принципиальные вопросы: область существования значений скин-фактора S и его принадлежность, неопределенность положительного и отрицательного знака его значений. Отсутствие строгой теории вывода его формулы. В связи с этим не были решены проблемы  качества вскрытия пласта, прогнозирования его энергетического состояния, фильтрационных свойств, определения продуктивности, текущего и потенциального дебита и коэффициента нефтеотдачи пласта в целом. Это было время глубокого кризиса в области подземной гидродинамики.         

Допущенные ошибки в формулах (1 и 2), а также в формулах для расчета базовых гидродинамических  параметров пласта и несоответствие расчетов, выполненных по указанным формулам промыслово-экспериментальным данным послужили толчком к созданию новой парадигмы подземной гидродинамики – реальной гидродинамической модели пласта [3,4,7].        

В работах [3;4] приводится подробный вывод формулы для определения ΔРs с учетом зональной неоднородности пласта:

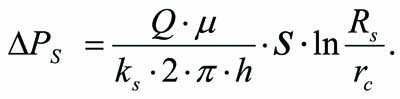
Указываются исторические ошибки и заблуждения, допущенные в формулах для определения скин-фактора, потери давления и притока в скин-слое при фильтрации жидкости. В связи с этим дается подробный и последовательный аналитический вывод его формулы. 1-Аналитический вывод формулы скин-фактора подтверждается в пяти вариантах выводами: 2- через индикаторные линии «дебит – давление», 3 — «дебит – уровень», 4 — по значениям забойного давления и 5 — потенциального дебита, 6 — приводится вывод формулы скин-фактора для зонально-неоднородного пласта [3,4,5].  Выведена зависимость для оценки влияния радиуса скин-слоя и коэффициента проницаемости на величину притока жидкости в скважину.       

Базовыми параметрами для составления гидродинамической модели пласта являются реальное значение потери давления ΔРs при фильтрации скважинной жидкости в околоскважинном пространстве, значение скин-фактора S, коэффициенты продуктивности К и проницаемости пласта k; пластовое Рпл и забойное Рз давления, динамический уровень скважинной жидкости hд, текущий приток Qж, потенциальный дебит Qпот и математические формулы для их определения.        

На основе теоретических и прикладных исследований, выполненных в области подземной гидродинамики и совместной работы пласта, скважины и подъемного (лифтового) оборудования определены и установлены фундаментальные зависимости всех базовых гидродинамических параметров пласта, скважины и насосного (лифтного) оборудования для оценки состояния околоскважинного пространства продуктивного горизонта и для оценки состояния зонально-неоднородного пласта [3…9]

Фундаментальные зависимости (формула Тима) для оценки состояния околоскважинного пространства продуктивного пласта [4…7]:

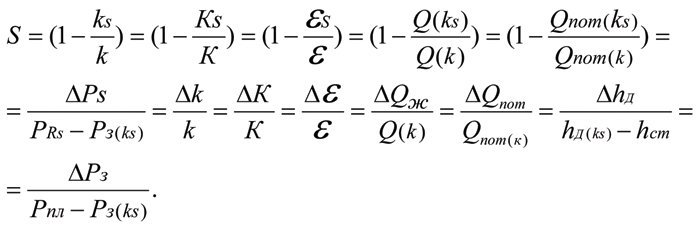
Фундаментальные зависимости (формула Тима) для оценки состояния зонально — неоднородного пласта:

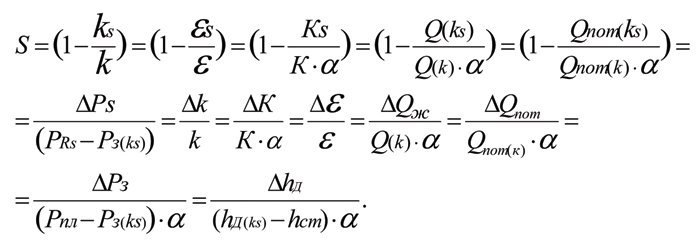
где α — коэффициент неоднородности пласта, как коэффициент пропорциональности, учитывающий неоднородность пласта по проницаемости.        

Система «Пласт-скважина-насосное оборудование» — как единая, неразделимая гидродинамическая система, взаимосвязанная фундаментальными зависимостями, отражающими единство и взаимосвязь всех гидродинамических параметров этой системы» подтверждаются математическими доказательствами и выводами всех базовых гидродинамических параметров пласта и их взаимосвязь фундаментальными зависимостями [3…9]. В этих работах приводятся подробные и последовательные доказательства всех положений «Теоремы Тима». «Теорема Тима» гласит, что «Любые изменения проницаемости продуктивного пласта приводят к пропорциональному изменению его продуктивности, гидропроводности, забойного давления, динамического уровня жидкости, текущего притока и потенциального дебита, а безразмерные относительные их величины равны между собой».

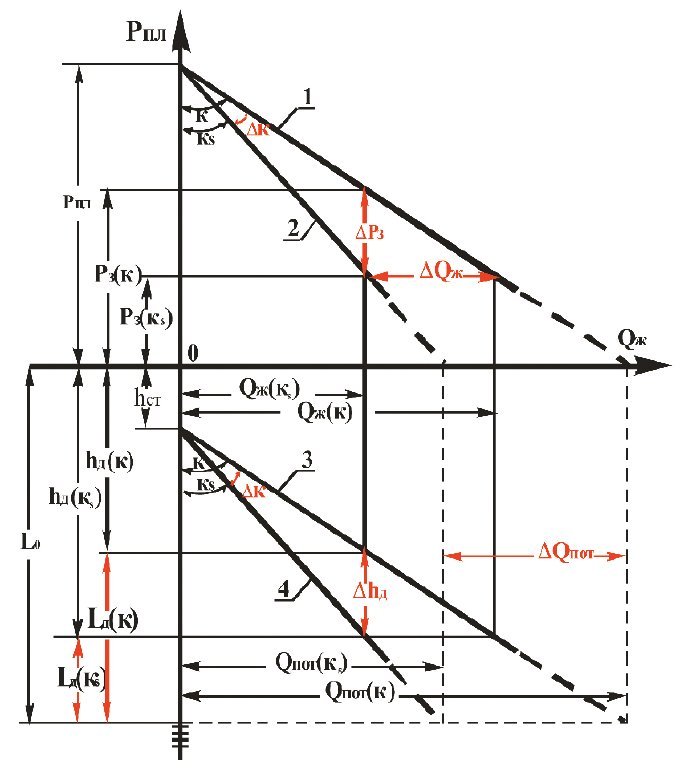
Рис. 1. Полная геометрическая интерпретация фундаментальных зависимостей и взаимосвязь гидродинамических параметров пласта и скважины, подтверждающая Теорему Тима: 1 — индикаторная линия Рз=f(Qж(к)); 2 — индикаторная линия Рз=f(Qж(кs));  3 — индикаторная линия hд=f(Qж(к));
4 — индикаторная линия hд=f(Qж(кs));  К – коэффициент продуктивности при естественной проницаемости пласта k; Кs — коэффициент продуктивности при ухудшенной проницаемости пласта ks; Qж(к) – приток жидкости при продуктивности пласта К; ΔК – снижение продуктивности в результате ухудшения проницаемости пласта от k до ks; Qж(кs) – приток жидкости при продуктивности пласта Кs;  ΔQж – снижение притока в результате ухудшения продуктивности пласта от К до Кs; hст – статический уровень жидкости в скважине; hд(к) – динамический уровень жидкости в скважине при продуктивности пласта К; hд(кs) – динамический уровень жидкости в скважине при продуктивности пласта Кs; Δhд – снижение динамического уровня жидкости в скважине в результате ухудшения продуктивности пласта от К до Кs; L – глубина скважины до верхних перфорационных отверстий; Lд(к) –динамическая глубина при продуктивности пласта К; Lд(кs) –динамическая глубина при продуктивности пласта Кs;  ΔРз  – снижение забойного давления в результате ухудшения продуктивности пласта от К до Кs; Qпот(к) – потенциальный дебит при продуктивности пласта К; Qпот(кs) – потенциальный дебит при продуктивности пласта Кs; ΔQпот – снижение потенциального дебита в результате ухудшения продуктивности пласта от К до Кs.        

В работах [4-9] дается критический анализ общепринятой формулы для определения притока жидкости к забою реальной скважины, конкретно указываются допущенные ошибки и в четырех вариантах приводится вывод формулы для определения притока жидкости к забою реальной скважины:

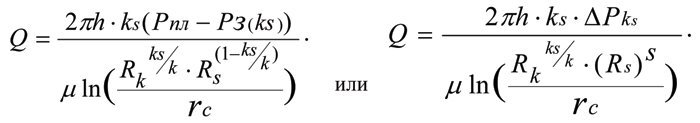
Фундаментальные зависимости (формулы Тима) полностью описывают, а теорема Тима доказывает реальную гидродинамическую модель продуктивного пласта.      

Фундаментальные зависимости гидродинамических  параметров системы «Пласт-скважина — насосное оборудование» должны быть использованы для проведения  количественной оценки и полного анализа состояния пласта, геофизических,  гидродинамических и технологических исследований (ГИС, ГДИС и ТИC), и всестороннего обоснования технологических и гидродинамических параметров при разработке программного обеспечения для инновационного проектирования процессов разработки нефтегазовых месторождений.

2. Квантованные поля продуктивного пласта – реальный материальный мир, физический природный объект     

В большинстве технических системах и технологических процессах приходится рассматривать одновременно совместное действие механических, тепловых, электрических, магнитных, оптических и гравитационных полей и их взаимосвязь. Для установления взаимосвязи между различными физическими полями важное значение имеет их размерность, принятая в единой системе единиц измерения.         

Продуктивный пласт находится под динамическим воздействием множеств геофизических (мульти) полей: геомеханического, гидродинамического, геомагнитного, электродинамического, геотермодинамического, гравитационного, волнового, оптического  и их производных. Значения параметров этих геофизических полей находятся в полной взаимосвязи и зависят от пространственной неоднородности и временной изменчивости состояния всей системы.

Эти поля можно разделить на две группы:

1. Геомеханическое и гидродинамическое поля. Под термином этих «полей» следует понимать часть пространственного объема горной породы пласта, находящегося под всесторонним  сжатием горного давления, характеризующее его напряженное состояние, прочность, упругость, устойчивость, проницаемость, пористость, пластовое давление, реологические параметры пластовой среды и т.д. Для геомеханических и гидродинамических задач понятие поля принимается чисто условно для составления математической модели действующей системы.

2. Электромагнитное и гравитационное поля. Эти поля, в отличие от первый группы, представляют реальные материальные объекты элементарных частиц. За электромагнитное поле отвечают элементарные частицы – электроны, протоны, нейтроны, кварки и их распад. Взаимосвязь этих частиц составляет три фундаментальные взаимодействия: притяжение электрона к ядру – электромагнитное взаимодействие. Взаимное притяжение кварков (внутриядерное взаимодействие) – пример сильного взаимодействия. Распад кварка и свободного нейтрона – бета распад пример слабого взаимодействия. Кроме трех фундаментальных взаимодействий огромную роль в природе имеет  четвертое фундаментальное взаимодействие, это взаимное притяжение всех частиц друг к другу в гравитационном поле. За гравитационное поле отвечают элементарные частицы – гравитоны.

Этих полей назовем «квантованными полями продуктивного пласта». Квантованное поле представляет собой природную реальность, материальный объект, который обладает энергией, инерцией и тяготением. Совокупность силовых линий квантованных полей в данной точке пространства образует так называемое потенциальное поле. Для потенциального поля справедливы два важных свойства. Первое – принцип суперпозиции, состоящий в том, что действие группы источников, создающих потенциальное поле может быть найдено последовательным векторным суммированием величин, создаваемых отдельно каждым из источников поля.  

Второе важное свойство – принцип максимума для потенциального поля. Значение максимума или минимума потенциала может достигаться только на поверхности источников поля или в бесконечности.                 

Ква́нтовая электродина́мика  (КЭД) — квантовая теория  электромагнитных взаимодействий наиболее разработанная часть квантовой теории поля. В классической электродинамике рассматривают только непрерывные свойства электромагнитного поля. Квантовая электродинамика основана на  том, что электромагнитное поле обладает также и прерывными (дискретными) свойствами, носителями которых являются кванты поля —фотоны. Взаимодействие электромагнитного излучения с заряженными частицами рассматривается в квантовой электродинамике как поглощение и испускание частицами фотонов.  Квантовая электродинамика, как фундаментальная квантовая теория поля была создана в 1940-х годах в работах Р. Фейнмана [10]. Это была первая теория поля взаимодействия заряженных элементарных частиц в магнитном поле. Квантовая электродинамика количественно объясняет эффекты взаимодействия полей с веществом, а также последовательно описывает электромагнитные взаимодействия между заряженными частицами. Электромагнитное поле (и его изменение со временем) описывается в электродинамики посредством системы четырех легендарных векторных уравнений Максвелла, где  электрическое и магнитное поле рассматривается как проявления единого электромагнитного поля. В квантовой механике полная энергия взаимодействия электрически заряженных частиц определяют оператором Гамильтона: Так, оператор Гамильтона атома с зарядом ядра Z имеет вид [11]:

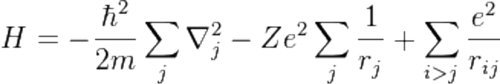
Здесь m — масса электрона, е — его заряд, rj — абсолютная величина радиус-вектора j-го электрона, ħ – постоянная Планка. Первое слагаемое выражает кинетическую энергию электронов, второе слагаемое — потенциальную энергию кулоновского взаимодействия электронов с ядром и третье слагаемое — потенциальную кулоновскую энергию взаимного отталкивания электронов. Суммирование в первом и втором слагаемом ведется по всем Z электронам. В третьем слагаемом суммирование идёт по всем парам электронов, причём каждая пара встречается однократно [12]. Константа Планка ħ, значение которой фиксирована и равна 6,626 x 10–34 Дж·с — это порция электромагнитной энергии, соответствующая одному кванту. Постоянная Планка ħ определяет границу между макромиром, где действуют законы механики Ньютона, и микромиром, где действуют законы   квантовой механики.

Постоянная Планка ħ указывает нам нижний предел пространственных величин, после которого нужно учитывать эффекты квантовой механики.

2.1. Квантовая электродинамика продуктивного пласта – базовая основа подсчета структурных запасов нефти.      

В этой работе впервые сделана попытка использовать информативность двойного электрического слоя (ДЭС), возникающего в капиллярах и трещинах породы пласта. Двойной электрический слой возникает при контакте двух фаз, из которых одна является жидкой. Стремление системы понизить поверхностную энергию приводит к тому, что частицы на поверхности раздела фаз ориентируются особым образом. Вследствие этого контактирующие фазы приобретают заряды противоположного знака, но равной величины, что приводит к образованию двойного электрического слоя (рис.2).

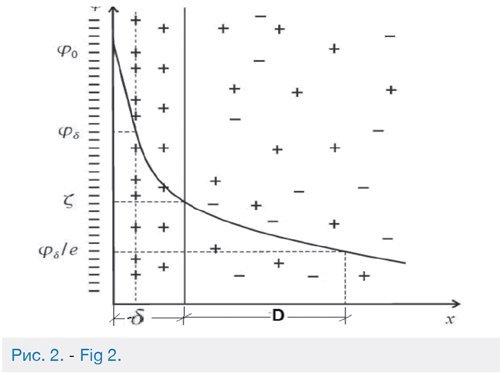
Образующийся двойной слой можно подразделить на плотную часть δ (слой Гельмгольца), образуемый ионами, прилегающими непосредственно к поверхности стенки капилляров породы, и диффузную часть (слой Гуи) D. В результате электростатического притяжения ионов заряженной поверхностью, с одной стороны, и хаотического теплового движения молекул, под влиянием которого ионы стремятся равномерно распределиться в нефти, – с другой, ионная часть приобретает диффузное строение. Концентрация ионов, несущих заряд, противоположный заряду поверхности породы, уменьшается по мере удаления от поверхности, а концентрация ионов, имеющих заряд, одинаковый по знаку с зарядом породы, возрастает по мере удаления от поверхности (рис.2). Слой Гельмгольца или адсорбционный слой, примыкающий непосредственно к межфазной поверхности имеет толщину δ, равную радиусу потенциалопределяющих ионов [13].

Общая толщина диффузного слоя D, зависит от целого  ряда фундаментальных констант:                   

где ε – абсолютная диэлектрическая проницаемость жидкости, R – постоянная Больцмана, Т – абсолютная температура, е – заряд электрона, N_A – число Авогадро, C_i — концентрация катионов различной природы, Z_i – валентность катионов. В этой формуле чрезвычайно важной является константа  Больцмана R.         

Если постоянная Планка ħ определяет границу между макромиром, где действуют законы механики Ньютона, и микромиром, где действуют законы квантовой механики, то константа R напрямую связывает характеристики микромира с характеристиками макромира. Эту связь обеспечивает постоянная Больцмана R, равная 1,38 x 10^–23 Дж/К. Общую толщину D диффузного слоя определить сложно. Для практических расчетов принимают, так называемую эффективную толщину λ диффузионной части ДЭС. Эффективная толщина диффузного слоя λ – это расстояние, где потенциал на границе плотного и диффузного слоев падает в е (основание натурального логарифма) раз. Диффузный слой или слой Гуи, в котором находятся противоионы имеет толщину λ, которая зависит от свойств системы и может достигать больших значений. Величина λ определяется при математическом описании ДЭС выражением

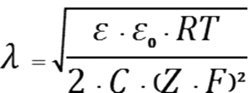  (4)

где ε — диэлектрическая постоянная;  R — газовая постоянная, 8,3 Дж\(моль*Кл); Т — абсолютная температура; Z — заряд иона; F — число Фарадея, 96400 Кл \ моль; С — концентрация ионов, моль – ион \ литр;  ε₀ — электрическая константа, 8,85 *10^-12Ф/м.          

Толщину плотного слоя δ – слоя Гельмгольца определяют по значению потенциалопределяющих ионов. Эффективную толщину диффузного слоя λ – по формуле (4). Общая толщина ДЭС составляет 1,5… 8.5 мкм [13]. По средним значениям δ и λ построен профиль скоростей течения нефти по капиллярам для различных значений притока (рис.3,4). Определены предварительные значения содержания нефти по структурным параметрам.

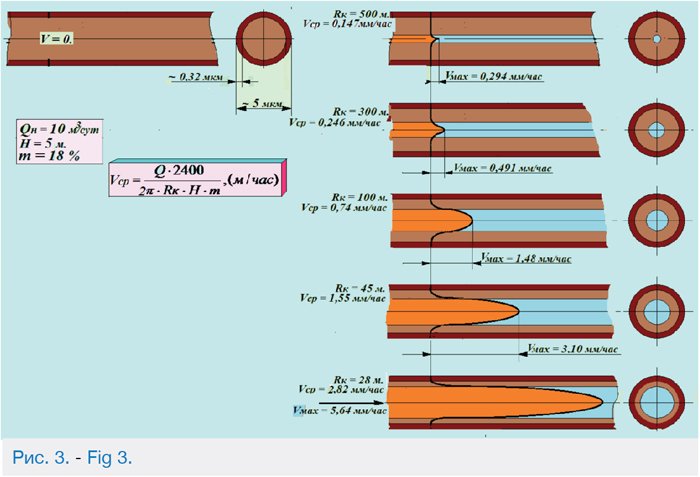
Рис. 3. Изменение профиля течения и толщины диффузного слоя при различных скоростях течения нефти по капиллярам, диаметром 5 мкм.           

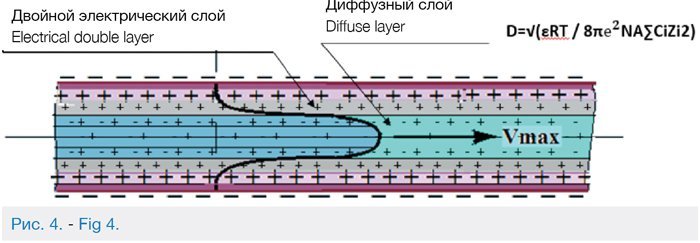
На рис. 4 схематично показан двойной электрический слой в капиллярах породы, содержащий слой Гельмгольца и диффузный слой.   

Слою Гельмгольца δ соответствует неподвижный пристенный (твердый) слой – абсолютно не извлекаемая часть нефти. По объему этот слой составляет 6…8% от геологических запасов и полностью входит в объем балансовых запасов.   

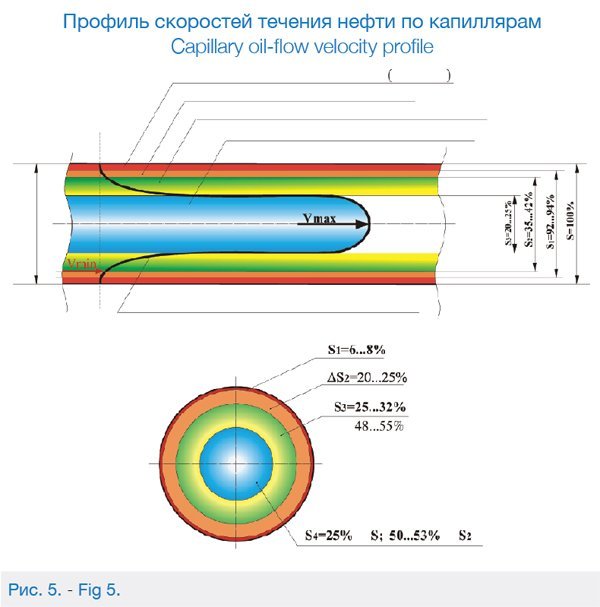
Высоковязкая малоподвижная прослойка нефти, переходящая к диффузному слою D составляет 20…25% от геологических запасов. Этот объем можно отнести практически к не извлекаемой части нефти при современном уровне развития техники и технологии добычи. Кроме того на эту прослойку все еще сильное влияние оказывает притяжение заряженных частиц плотного двойного электрического слоя Гельмгольца.       

Переходной слой – трудноизвлекаемая часть, относится к начальной области диффузного слоя D, где силы взаимного притяжения заряженных частиц начинают снижаться по экспоненте. Объем трудноизвлекаемой части составляет 25…32% от геологических запасов.      

Подвижная – извлекаемая часть нефти. При этом концентрация ионов, несущих заряд, противоположный заряду поверхности породы, уменьшается по мере удаления от стенки капилляра, а концентрация ионов, имеющих заряд, одинаковый по знаку с зарядом породы, возрастает. Сила притяжения и отталкивания заряженных ионов нейтрализуется.      

Объем подвижной — извлекаемой части составляет 25…35% от геологических запасов, без учета слоя Гельмгольца –35…45%.       

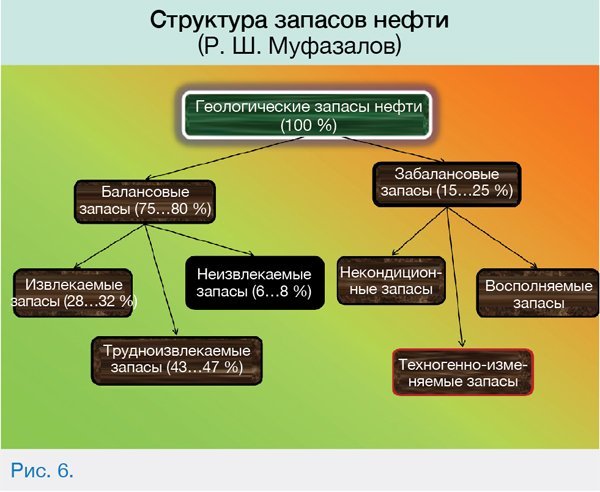
В структурных запасах (рис.6) объемы нефти высоковязкой малоподвижной прослойки и переходного слоя объединены и процентные соотношения указаны от доли балансовых запасов.

Краткое сведения об авторе :

Роберт Муфазалов

• 270 научных работ, из них:

• 117 изобретений;

• 13 монографий (научные книги);

• 4 учебников для вузов (с грифом минвуза);

• Заслуженный изобретатель Респ. Башкортостан;

• Изобретатель СССР;

• Отличник Министерства нефтяной промышленности СССР;

• Включен в энциклопедию «Инженеры Урала»;

• Член-корреспондент РАЕН;

• Участник более 30 международных конференций, конгрессов и всемирных выставок по новейшим и наукоемким технологиям.

Научные интересы:

квантовая геомеханика, подземная гидродинамика, гидравлика, нелинейная гидроакустика, техника и технология бурения, гидромеханика добычи нефти, нефтехимия, медицина — ( 8 патентов на изобретения),

разработка и создание высоких технологий для нефтегазохимического комплекса.

Литература

1. A. F. van Everdingen and W. Hurst. The Application of the Laplace Transformation to Flow Problems in Reservoirs. – Trans. AIME, Vol. 186, 1949. – pp. 305–24.

2. M. F. Hawkins, Jr. A note on the skin effect. – Trans. AIME, Vol. 207, 1956. – pp. 356–57.

3. Муфазалов Р. Ш. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта и их последствия. Часть 1, 2, 3. // Труды 12 – Международного симпозиума «Энергоресурсоэффективность и энергосбережение». – Казань: «Центр Оперативной Печати». – 2011. – С. 409–464. [R. Sh. Mufazalov. Historical errors and misconceptions at work in the oil reservoir hydrodynamics theory, and their consequences. Part 1, 2, 3. // Proceedings # 12 of the International Symposium titled “Power resource efficiency and power savings.” – Kazan: Tsentr Operativnoy Pechati. – 2011. – pp. 409–464.]

4. Муфазалов Р. Ш. Скин-фактор. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта. – Георесурсы. № 5. – 2013. – С. 34–48. [R. Sh. Mufazalov. Skin factor. Historical errors and misconceptions at work in the oil reservoir hydrodynamics theory. – Georesources. Issue # 5. – 2013. – pp. 34–48.]

5. R. Sh. Mufazalov. Skin factor and its importance for evaluating borehole environmental conditions for a productive formation. // «ROGTEC», Oil & Gas Magazine. Issue # 19. – pp. 18–36.

6. Муфазалов Р. Ш. Скин-фактор. Фундаментальные зависимости параметров пласта, скважины, оборудования и фундаментальное заключение. // Материалы научно-практической конференции «Актуальные вопросы разработки нефтяных месторождений на поздних стадиях». Уфа: Изд-во УГНТУ. – 2010. – с. 80–93. [R. S. Mufazalov. Skin factor. Fundamental relationships between the reservoir, well, and equipment parameters and a fundamental conclusion. // Materials of the International Research & Practice Conference titled “Topical issues of mature oil and gas fields development.” Ufa: UGNTU Publishing House. – 2010. – pp. 80–93.]

7. Муфазалов Р. Ш. Исторические ошибки и заблуждения, допущенные в теории подземной гидродинамики, и ее новая парадигма. // Материалы международной научно-практической конференции «Инновации в разведке и разработке нефтяных и газовых месторождений». – Казань: Изд-во НПО «Ихлас». – 2016. Т. 2. – с. 58–63. [R. Sh. Mufazalov. Historical errors and misconceptions at work in the theory of subsurface hydrodynamics and a new paradigm for it. // Materials of the International Research & Practice Conference titled “Innovation in the exploration and development of oil and gas fields.” – Kazan. Ikhlas Publishing House. – 2016. Vol. 2. – pp. 58–63]

8. R. Sh. Mufazalov. Skin factor. Relationships, conclusions, and the formula for the key hydrodynamic parameters. // ROGTEC, Oil & Gas Magazine. Issue # 41. – pp. 74–88.

9. Муфазалов Р. Ш. Теорема Тима. Фундаментальные зависимости гидродинамических параметров пласта и скважины, и их взаимосвязь – основа инновационного проектирования процессов разработки нефтегазовых месторождений. // Материалы Международной научно-практической конференции «Моделирование геологического строения и процессов разработки – основа успешного освоения нефтегазовых месторождений». – Казань: Изд-во «Слово». – 2018. – с. 67–69. [R. Sh. Mufazalov. Tim’s Theorem. Fundamental dependences among the hydrodnamic parameters of the reservoir and the well and their interrlationships as a basis for innovative process design solutions for oil and gas field development. // Materials of the International Research & Practice Conference titled “Modeling the geological structure and development processes as a basis for successful exploitation of oil and gas fields. – Kazan. Slovo Publishing House. – 2018. – pp. 67–69.]

10. Фейнман Р. Квантовая электродинамика. 3-е изд. – М.: Наука. – 2004. – 255 с. [R. Feynman. Quantum electrodynamics. 3rd ed. – Moscow: Nauka. – 2004. – 255 pp.]

11. Грибов В. Н. Квантовая электродинамика. – Ижевск: РХД. – 2001. – 288 с. [V. N. Gribov. Quantum electrodynamics. – Izhevsk: RKhD. – 2001. – 288 pp.]

12. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. – М.: Физматлит. – 2002. – 720 с. [V. B. Berestetsky, Ye. M. Lifshits, L. P. Pitayevskiy. Quantum electrodynamics. – Moscow: Fizmatlit. – 2002. – 720 pp.]

13. Дамаскин Б. Б., Петрий О. А. Введение в электрохимическую кинетику. 2-е изд. – М.: Наука. – 1983. [B. B. Damaskin, O. A. Petriy. Introduction to electrochemical kinetics. 2nd ed. – Moscow: Nauka. – 1983.]

14. Муфазалов Р. Ш. Квантовая электродинамика пласта – фундаментальная основа подсчета структурных запасов нефти. // Материалы Международной научно-практической конференции «Моделирование геологического строения и процессов разработки – основа успешного освоения нефтегазовых месторождений». – Казань: Изд-во «Слово». – 2018. – с. 296–300. [R. Sh. Mufazalov. Quantum electrodynamics of the reservoir as a basis for successful exploitation of oil and gas fields. // Materials of the International Research & Practice Conference titled “Modeling the geological structure and development processes as a basis for successful exploitation of oil and gas fields. – Kazan. Slovo Publishing House. – 2018. – pp. 296–300.]