Программное решение для автоматической оптимизации логистики во время бурения и освоения скважин

Оптимизация логистики во время бурения и освоения скважин состоит в построении оптимального расписания для всех трудовых ресурсов. Построение оптимального расписания позволяет существенно сократить время и затраты, связанные с геологическими и технологическими рисками.  Для этого необходимо иметь соответствующие инструменты математического моделирования.

В статье приводится описание функциональности программного решения и результаты тестирования.

В данной работе методикой построения оптимального расписания является комбинация известных алгоритмов – метода ветвей и границ и симплекс-метода. В качестве входных данных выступает «начальное расписание», которое содержит: геометрию месторождения – расстановка скважин, расстояние между ними; список типов работ – тип работы, принадлежность к скважине, дата начала,  продолжительность работы и т.д.; ограничения на допустимость расписания – условия последовательности работ на одной скважине, условия одновременности работ на соседних скважинах и т.д. Программа позволяет выбрать параметр, по которому будет производиться оптимизация, время расчета и сценарий оптимизации. В качестве выходных параметров получаем список работ с указанием их типа, даты начала работы, продолжительности и принадлежности к скважине. Кроме того, получаем суммарный дебит и накопленную добычу на момент запуска куста скважин в эксплуатацию в сравнении с изначальным и оптимизированным расписанием.

Для удобного графического представления расписания применяются диаграммы Гантта [1]. Диаграммы бывают двух типов: загруженность оборудования конкретной работой от времени и выполнение типа работы на оборудовании. Типичный пример диаграммы Гантта представлен на рисунке 1.

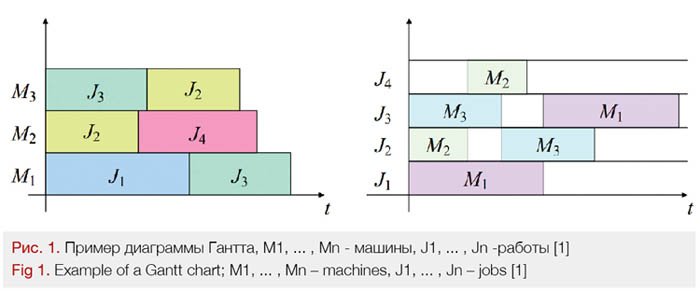
Важным ограничением при построении оптимального расписания является конечный шаг по времени. Это позволяет формулировать задачи в терминах дискретного программирования. Под задачей дискретного программирования понимается задача минимизации некоторой функции на множестве допустимых решений.

В основе модуля лежит вариация симплекс-метода и метода ветвей и границ. Метод ветвей и границ относится к методам сокращенного перебора [2, 3, 4]. Van den Akker J.M и др. [4] исследовали параметры приоритета расстановки работ на параллельных машинах и дали оценки критериев для определенных задач. В работе [3] авторы разработали и алгоритм приближенного решения задачи минимизации затраченного времени с повышением точности в зависимости от времени расчета. Alex J. Ruiz-Torres и др. [2] представили алгоритм для минимизации времени работы на одной машине.

Раздел целочисленное программирование в ограничениях включает в себя несколько областей программирования. Tobias Achterberg и др. [5,6] приводят обзор актуальных алгоритмов в целочисленном программировании в ограничениях на данный момент. Наиболее известным и широко применяемым на практике для решения общей задачи программирования в ограничениях является симплекс-метод. Задача состоит в оптимизации линейного функционала на многомерном пространстве при заданных линейных ограничениях.

Ограничения, накладываемые на переменные, образуют область, являющуюся многомерным многогранником. Решением задачи является одна из вершин многогранника, а поиск ведется перебором соседних граней. Исследования, проводимые в работах [7,8,9] выявили высокую универсальность симплекс-метода.

Постановка задачи

Как ранее упоминалось, для решения задачи необходимо выбрать конечный шаг по времени.  В данной постановке был использован шаг, равный одним суткам и общая длина расписания в 365 дней, как компромисс между скоростью и точностью.

Куст месторождения состоит из 24 скважин, сгруппированных в кластеры по 4 (рис 2), расстояния между скважинами в кластере – 5м., между крайними скважинами кластеров – 15 м. Трудовые ресурсы представлены 5-ю типами бригад: бурения —  1 бригада, КРС – условно не ограничено, ГРП — 1 флот, ГНКТ — 1 флот, «Обвязка» — 1 бригада. Особенностью работ типа «Обвязка» является то, что они проводятся одновременно на всем кластере. Расстояние между любыми двумя бригадами не должно быть меньше 30 м., кроме работ типа «Обвязка», для них – 25 м.

Каждой бригаде соответствует свой список работ. Общий список работ состоит из 8-ми операций: (бурение направления-кондуктора, бурение эксплуатационной колонны, бурение хвостовика) – бригада бурения, (подготовка к ГРП, освоение) – бригады КРС, (проведение ГРП) – флот ГРП, (ГНКТ) – флот ГНКТ, («Обвязка») – бригада «Обвязка».

Конечной целью оптимизации является минимизация или максимизация целевой функции. В данной работе оптимизируется три параметра:

• Максимизация накопленной добычи: 1) на конец года, 2) на рассчитанный период — 365 дней.
• Минимизация по среднему значению срока введения скважины в эксплуатацию (RRSU – Rig Release to Startup).
• Минимизация «простоя» критических ресурсов (работ типа ‘frac’ и ‘coil’). Необходимо, чтобы работы данного типа выполнялись как можно плотнее для всего куста, для уменьшения стоимости данных работ.

Программное решение

Решение оформлено в виде программного пакета. Программный пакет имеет интерфейс, состоящий из
6 основных панелей, представленных на рисунке 3.

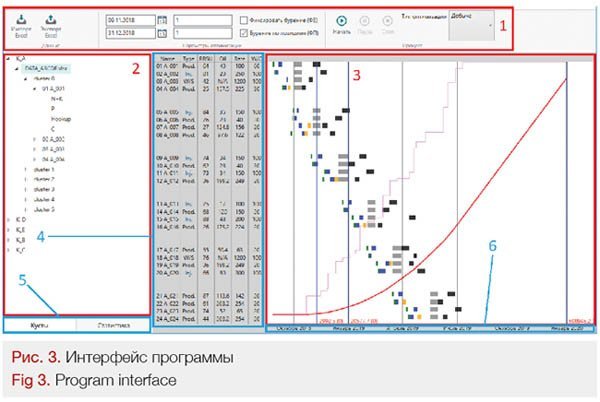
На панели инструментов (1) представлен функционал ввода и вывода данных, параметры оптимизации и непосредственно запуск оптимизации. Окно данных (2) — позволяет выводить данные расписания в виде иерархического списка или как таблицы статистики переключением панели данных (5). Окно визуализации расписания (3) выводит данные в виде расписания по скважинам. Цвет прямоугольника обозначает тип работ, положение — временные рамки. Кроме работ в окне приведены суточный и суммарный накопленный дебеты. Краткая информация по скважине доступна в таблице данных (4). Содержит: имя, тип, время введения в эксплуатацию, дебет и степень обводненности. При необходимости можно настроить удобный масштаб по времени, используя временную шкалу (6).

Апробация

Для апробации разработанного ПО использовались данные по 5 кустам (A, B, C, D, E), которые представлены в виде начального расписания по скважинам.

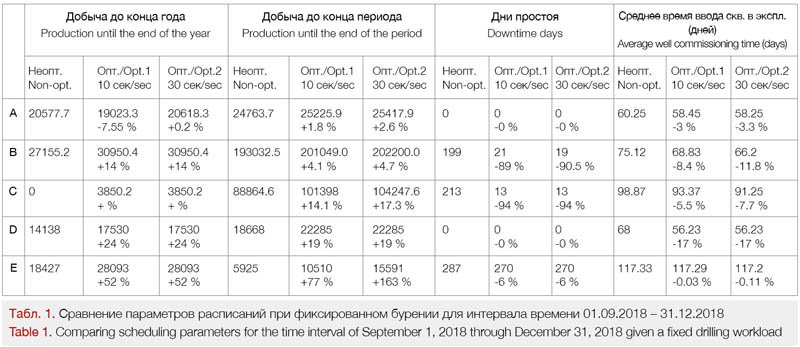
В таблице 1 приведено сравнение по четырем параметрам оптимизации: суммарная добыча до конца года (31.12.2018), суммарная добыча до конца периода (365 дней с момента начала работ), дни простоя и среднее количество дней для введения скважины в эксплуатацию (RRSU).

В первом варианте оптимизации время расчета составляет 10 секунд, во втором – 30 секунд.

Как видно, в большинстве случаев происходит улучшение параметра оптимизации. Но в примере A-Опт. 1 для добычи до конца года параметр уменьшился. Это связано с особенностями оптимизационного алгоритма, а точнее со временем его работы. Сравнивая Опт. 1 и Опт. 2 можно отметить, что увеличение времени расчёта улучшают показатели оптимизации.

При этом наблюдается большой разброс относительных значений результатов оптимизации для разных кустов, так как в общем случае на качество оптимизации, помимо времени расчета влияют сложность модели куста и начальное расписание.

Выводы и результаты

Созданный программный пакет реализует цели и сценарии оптимизации с учетом ограничений, заявленных в постановке задачи.

Тестирование модели оптимизации показало улучшение показателей относительно начального расписания по добыче до +163%, по сокращению дней простоя до -94% и по времени ввода скважины в эксплуатацию до -17%.

На данном этапе модель подходит для решения только ограниченного круга задач, в связи с чем она нуждается в обобщении постановки и расширении функциональности.

Дальнейшее расширение модели:

• Добавление возможности работы с форматами входных и выходных данных.
• Обобщение геометрии модели (расстояния между скважинами, группировка по кустам, по кластерам).
• Введение рисков работ, стоимости работ.
• Введение подготовительных работ и работ по перемещению оборудования.
• Уменьшение шага по времени.
• Учет падения добычи со временем, учет взаимовлияния скважин.
• Введение в схему оптимизации цены на продукцию.

Список литературы

1. У. Кларк. Графики Гантта. Учёт и планирование работы. 5-е издание. — Москва: Техника управления, 1931.

2. Alex J. Ruiz-Torres, Giuseppe Paletta, Eduardo Perez.  Parallel machine scheduling to minimize the makespan with sequence dependent deteriorating effects. Computers & Operations Research 40 (2013) 2051–2061.

3. Klaus Jansena, Monaldo Mastrolilli. Approximation schemes for parallel machine scheduling problems with controllable processing times. Computers & Operations Research 31 (2004) 1565 – 1581

4. Van den Akker J.M., Hoogeveen J.A., van de Velde S.L. Parallel machine scheduling by column generation // Oper. Res.– 1999.– V. 47, N 6.–P. 862 – 872.

5. SCIP: Solving Constraint Integer Programs Tobias Achterberg. Mathematical Programming Computation, Volume 1, Number 1, Pages 1–41, 2009.

6. Constraint Integer Programming: a New Approach to Integrate CP and MIP. Tobias Achterberg, Timo Berthold, Thorsten Koch, Kati Wolter, Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, CPAIOR 2008, LNCS 5015, Pages 6–20, 2008

7. Bland, Robert G. (May 1977). «New finite pivoting rules for the simplex method». Mathematics of Operations Research. 2 (2): 103–107

8. Maros, István (2003). Computational techniques of the simplex method. International Series in Operations Research & Management Science. 61. Boston, MA: Kluwer Academic Publishers. pp. 325

9. Spielman, Daniel; Teng, Shang-Hua (2001). «Smoothed analysis of algorithms: why the simplex algorithm usually takes polynomial time». Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing. ACM. pp. 296–305.

Authors:

Д.М.Хамадалиев¹, Е.Н.Ульянов¹, В.Н. Ульянов², Д.О.Тайлаков², К.С.Сердюк², Р.З.Курмангалиев², С.А.Фролов², К.И.Нектягаев², Р.И.Вылегжанин², Е.Н.Павловский³

1. Салым Петролиум Девелопмент Н.В,

2. ООО «Новосибирский научно-технический центр»,

3. Лаборатория аналитики потоковых данных и машинного обучения НГУ