Теорема Тима: Фундаментальная основа новой парадигмы подземной гидродинамики Часть 2

«Тысячи путей ведут к заблуждению, к истине – только один».

Жан-Жак Руссо, 1712 – 1778.

Данная статья является продолжением первой части статьи, опубликованной в выпуске 57 журнала ROGTEC

Приводится критический анализ существующей концепции по определению притока жидкости к забою реальной скважины с зонально-неоднородностью пласта, конкретно указываются допущенные ошибки. Излагается в четырех вариантах вывод формулы для определения притока жидкости зонально-неоднородного пласта к забою реальной скважины. Формула для определения притока подтверждается выводами формулы притока по значениям забойного давления, с учетом потери давления в скин-слое, в контуре питания и по значению коэффициента проницаемости зонально-неоднородного пласта. Указываются ошибки, допущенные в формуле для определения эффективного (приведенного) радиуса скважины. Приводится новое определение эффективного (приведенного) радиуса скважины и дается вывод его формулы.

3. Ошибки и заблуждения, допущенные в формулах для определения притока к забою реальной скважины и приведенного (эффективного) его радиуса

Приток пластовой жидкости к забою идеальной скважины при плоско — радиальной фильтрации определяют по формуле Дюпюи

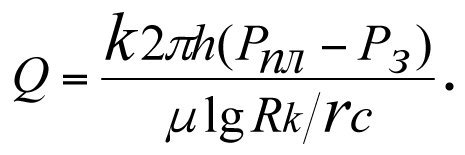  . (3.1)

Для определения притока к забою гидродинамически несовершенной (реальной) скважины в работах [1, 3] и других учебных и научных литературах, в т.ч. зарубежных, рекомендуют               

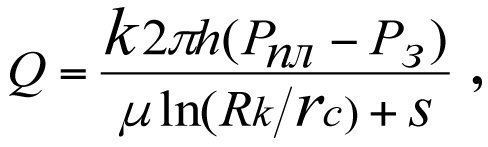  , (3.2)

где S – значение скин-фактора.

Щуров В.И. [6] для определения притока рекомендует формулу (3.2*), ничем не отличающуюся от (3.2), где значение С отражает гидродинамическое несовершенство по степени и характеру вскрытия продуктивного пласта.              

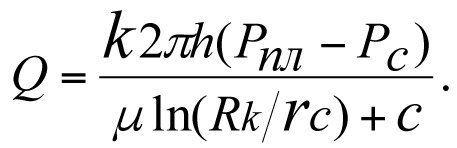  (3.2*)

Ипатов А.И., Кременецкий М.И. [4], рекомендуют (9.5.2.2), где

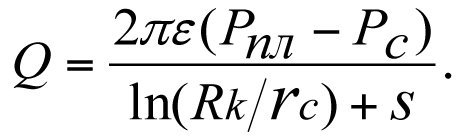  (3.3)

Закиров С.Н., Индрупский И.М., Закиров Э.С. и др. [5] считают наиболее строгой формой определения притока следующую формулу

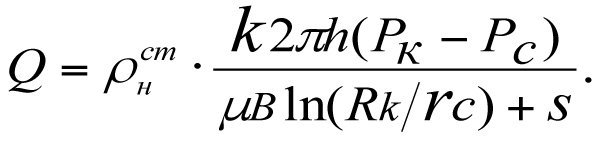  (3.3*)         

Из сравнения тривиальных формул (3.2), (3.2*), (3.3) и (3.3*) с формулой Дюпюи видно, что единственным отличием является дополнительное слагаемое в знаменателе S или С. В (3.3) главный определяющий параметр k спрятан под знак ε, а в (3.3*) дополнительно введенные параметры плотности ρн нефти и его объемный коэффициент В в стандартных условиях, не имеют никакого значения для определения притока зонально-неоднородного пласта.    

Принципиальными и грубыми ошибками в вышеуказанных формулах являются:

—  не учтен коэффициент проницаемости ks скин-зоны;

—  не учтена толщина скин-слоя R_s — r_с околоскважинного пространства;

— не учтены дополнительные потери давления ∆Рs в скин-слое в результате ухудшения проницаемости от k до ks;

—  не учтена зональная неоднородность пласта по проницаемости;

—  значение S, как коэффициент пропорциональности, нельзя суммировать, что является грубейшей математической ошибкой.   

Перечисленные ошибки являются следствием не только повторения исторических ошибок V. Everdingen A. F. & Hurst N. и Hawkins M.F. для вывода формулы притока, прежде всего — непонимания авторами этих формул элементарных законов подземной гидродинамики.     

Таким образом, в формулах (3.2), (3.2*), (3.3) и (3.3*) для определения притока зонально-неоднородного пласта не соблюдены физические законы гидродинамики пласта, нарушена математическая логика и допущены указанные серьезные ошибки. Вышеуказанные формулы (3.2), (3.2*), (3.3) и (3.3*) не пригодны для расчета дебита реальной скважины с зонально-неоднородной проницаемостью пласта и должны быть  исключены из учебников и учебных пособий подземной гидродинамики. В связи с этим в четырех вариантах излагается вывод формулы для расчета дебита (объемного притока) к забою реальной скважины.

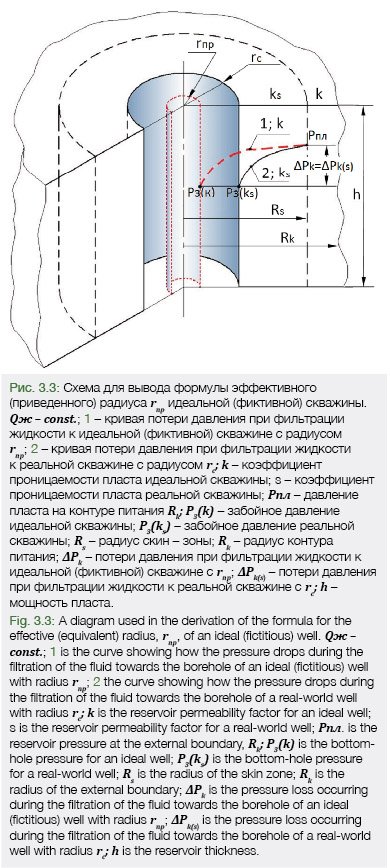
3.1. Вывод формулы для определения дебита реальной скважины с зонально-неоднородный проницаемостью пласта (рис. 3.1).

Вариант 1. Определение притока с учетом потери давления ∆Рs в скин-слои, Q – const.

Потери пластового давления ∆Рk при фильтрации жидкости к забою идеальной скважины с коэффициентом проницаемости k пласта  определяются формулой Дюпюи (кривая 1)                     

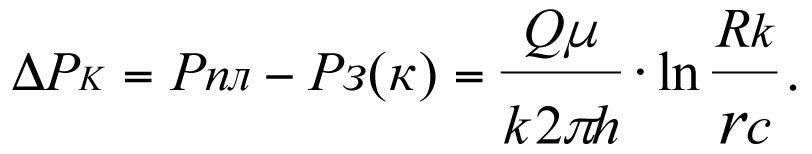  (3.4)                                                 

Дополнительные потери пластового давления ∆Рs в скин-слое с коэффициентом проницаемости ks при фильтрации жидкости к забою реальной скважины определяются формулой (см. часть 1, вывод формулы 1.13 и 1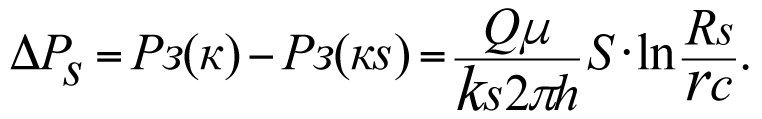.35)

  (3.5)

Все обозначения указаны на рис. 3.1.   

Общие потери пластового давления ∆Рks в зонально-неоднородном пласте (т.е. с учетом скин-слоя) составят

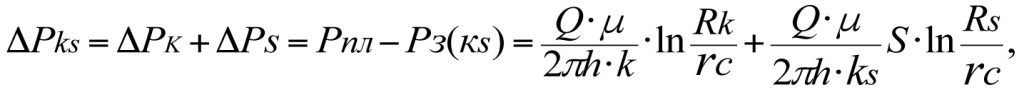(3.6)

или

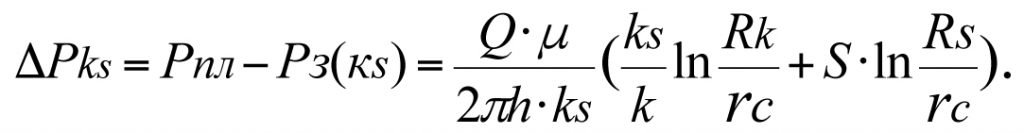(3.7)

Уравнению (3.7) соответствует кривая 2 на рис. 3.1. Из (3.7) получим формулу для определения объемного притока (дебита) к забою гидродинамически несовершенной (реальной) скважины

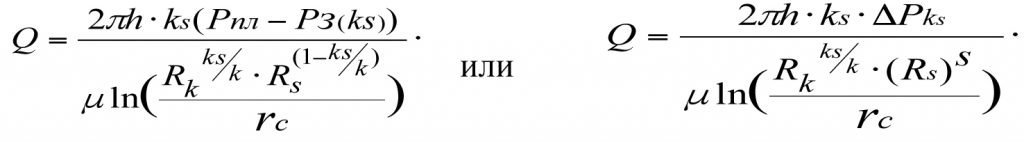  (3.8)                                                                                                                

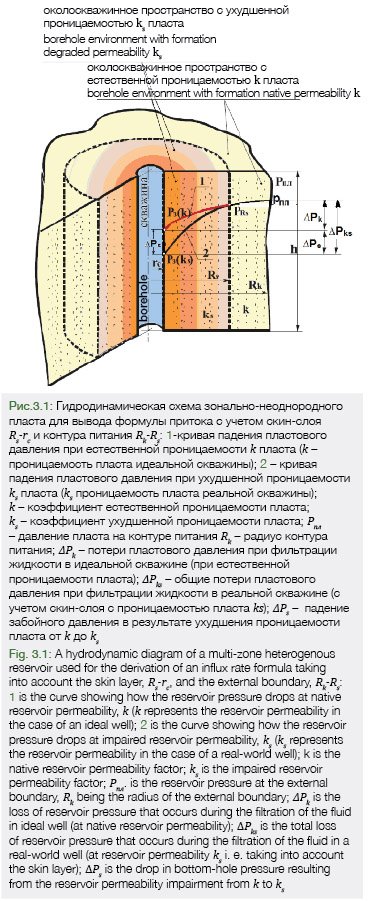
Вариант 2. Определение притока с учетом потери давления в контуре питания P_пл-P_Rs, (рис. 3.1, кривая 2), Q-const.

Потеря давления в контуре питания с проницаемостью k составит

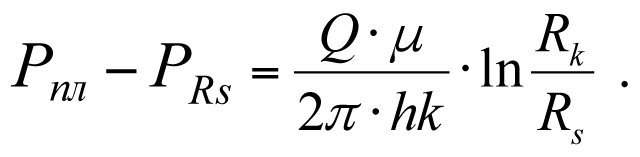(3.9)

Потеря давления в скин-слое с проницаемостью ks составит

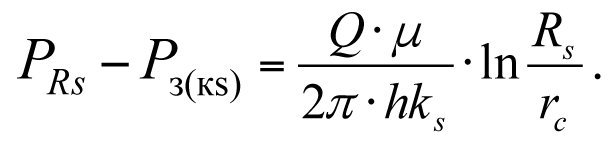(3.10)

При этом общие потери давления в околоскважинном пространстве составят

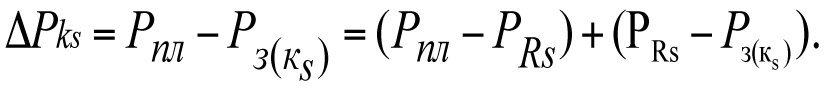   (3.11)

Подставляя значения (3.9) и (3.10) в (3.11), получим потери давления при фильтрации жидкости в зонально-неоднородном пласте по проницаемости

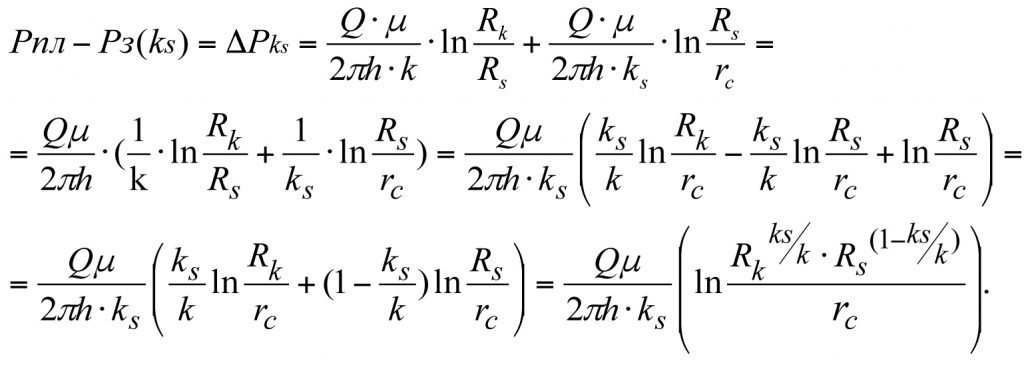  (3.12)

Из (3.12) получим формулу для определения притока к забою реальной скважины с зонально-неоднородной проницаемостью пласта

 (3.13)

Вариант 3. Определение притока зонально-неоднородного пласта через его среднее значение коэффициента проницаемости kср, (рис. 3.1).
Q –const.

Дебит идеальной скважины          

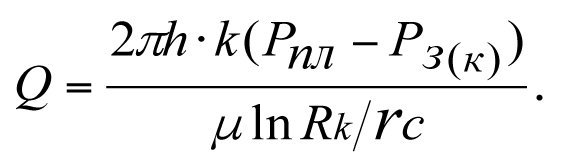  (3.14)

Дебит реальной скважины выразим через среднее значение коэффициента проницаемости kср. При этом пласт рассматриваем как однородный с коэффициентом проницаемости kср.                                        

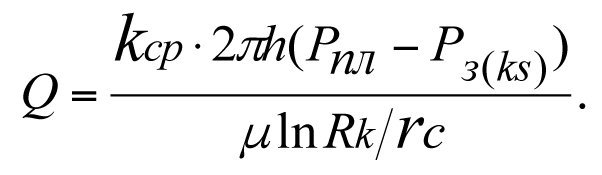 (3.15)        

Из равенства дебитов идеальной и реальной скважин и приравнивая правые части (3.14) и (3.15), запишем    

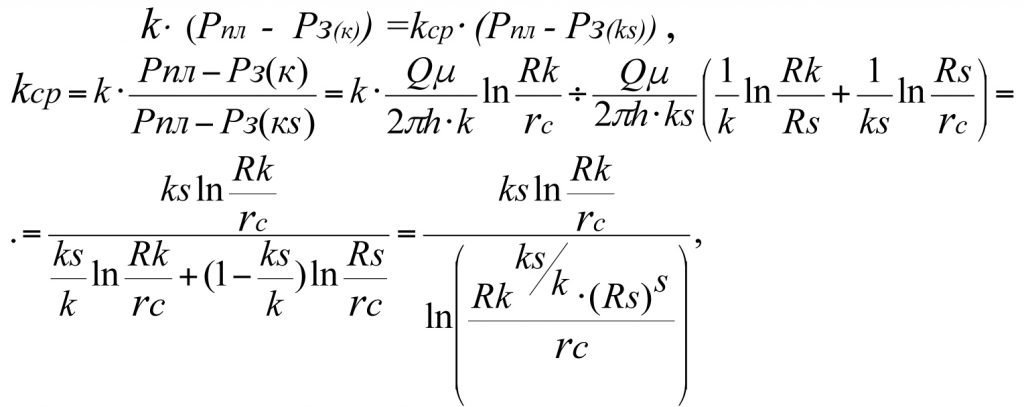
отсюда

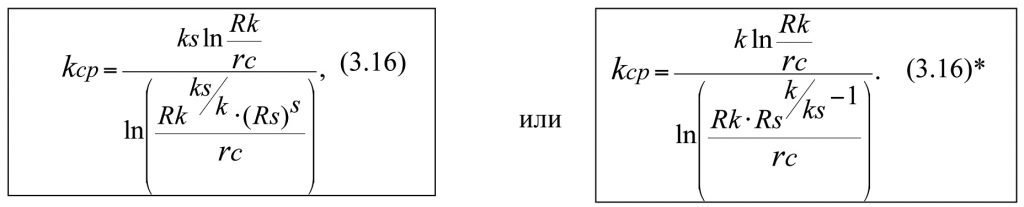
Формулы (3.16) и (3.16)* для определения kср эквивалентны.

Подставляя значение (3.16) в (3.15) получим дебит реальной скважины с зонально-неоднородной проницаемостью пласта

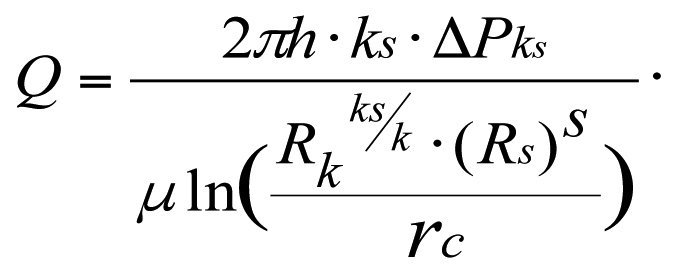  (3.17) 

Вариант 4. Определение дебита скважины с зонально-неоднородной проницаемостью пласта при равенстве забойных давлений,
Рз(кs) = Pз(к)= Рз; Рпл — Рз(кs) = Рпл — Рз(к)=
=Рпл — Рз=ΔРk-const.

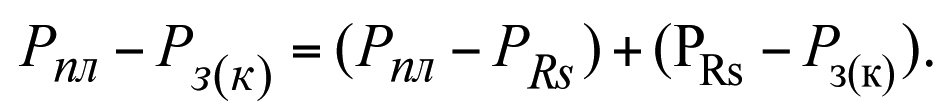
В интервале Рпл – РRs коэффициент проницаемости равен k, а в интервале PRs –Pзк – равен ks (см. рис. 3.1)     

Общие потери давления в интервале Рпл – Рз(к) составят     

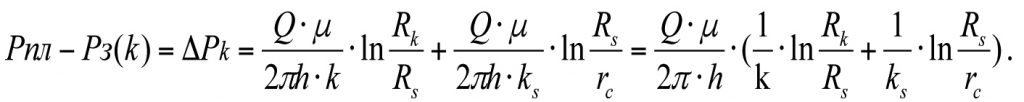 (3.18)

Из (3.18) получим

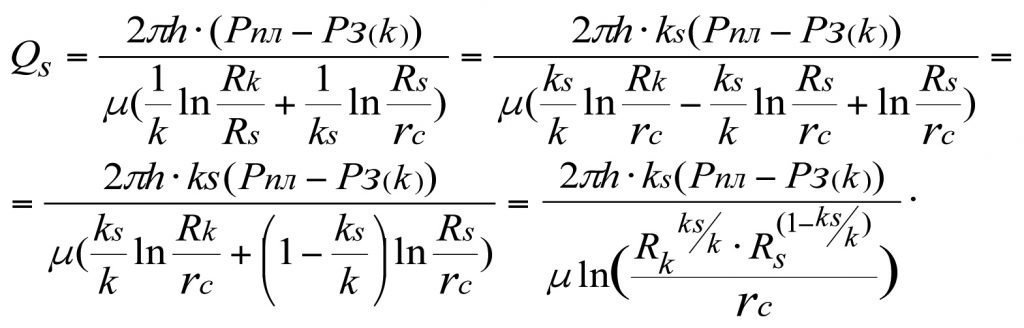
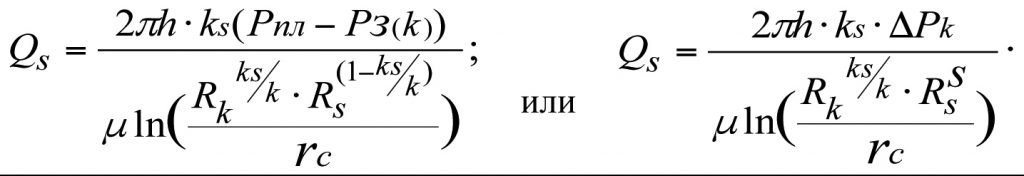  (3.19)

 Формулы (3.8), (3.13), (3.17) для определения притока к забою скважины с зонально-неоднородной проницаемостью пласта идентичные, а (3.19) – эквивалентна.

3.2. Потери притока к забою реальной скважины при снижении забойного давления от Рз(k) до Рз(ks), (пласт зонально-неоднородный по проницаемости).    

Приток при забойном давлении Рз(ks) составит (см. 3.13)

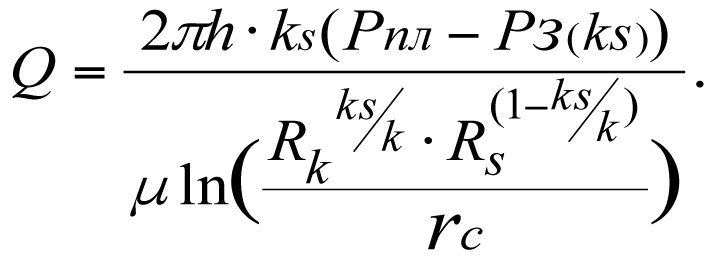  (3.20)         

Приток при забойном давлении Рз(k) составит (см. 3.19)

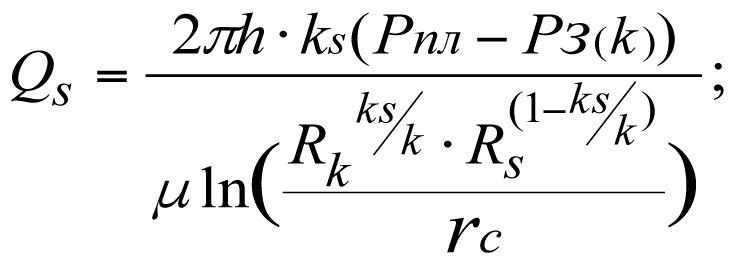 (3.21)    

Потеря притока при этом составит ΔQ = Q – Qs,

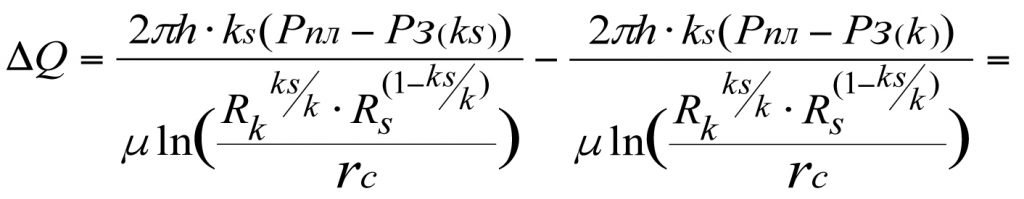
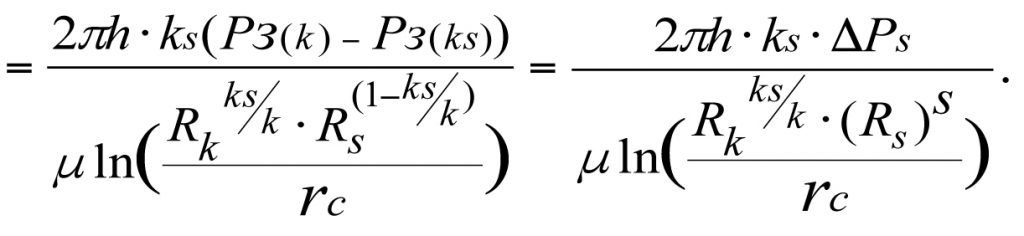
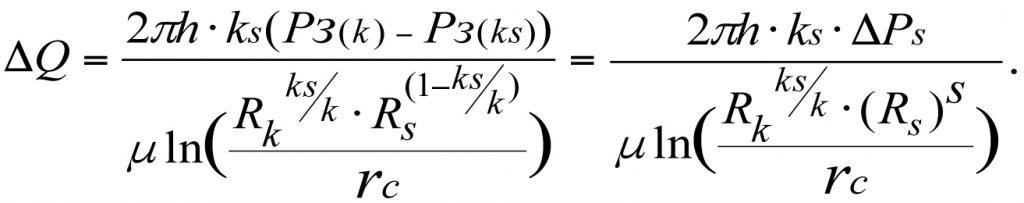   (3.22)    

Формула (3.22) показывает, что потеря давления в скин-слое на величину ΔPs приводит к пропорциональному снижению притока (дебита) на величину ΔQ.

3.3. Взаимосвязь между основными гидродинамическими параметрами скважины и коэффициентом проницаемости пласта

3.3.1. Взаимосвязь между коэффициентами продуктивности реальной скважины Ks и проницаемости ks зонально-неоднородного пласта.
Q-const.

Дебит реальной скважины при зонально-неоднородном пласте (3.8)

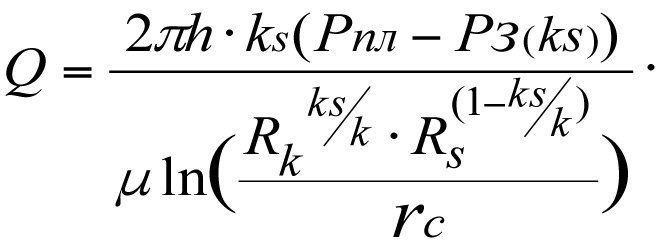(3.23)

Дебит идеальной скважины    

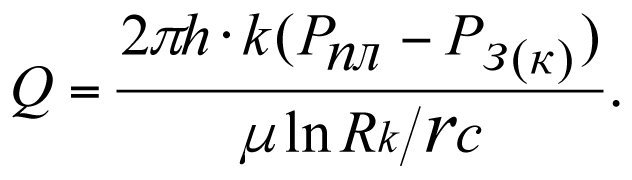(3.24)

При Q-const, приравнивая правые части (3.23) и (3.24), запишем

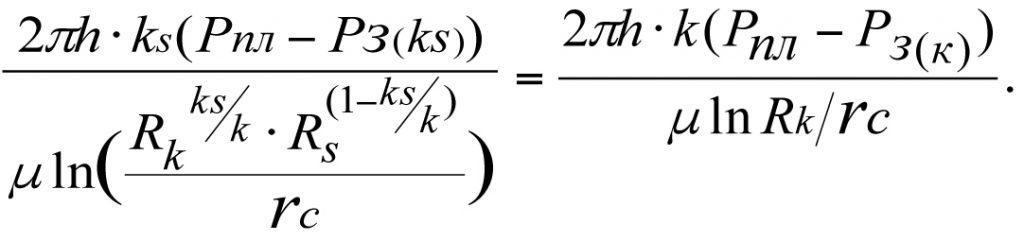
При этом коэффициент продуктивности Ks реальной скважины составит

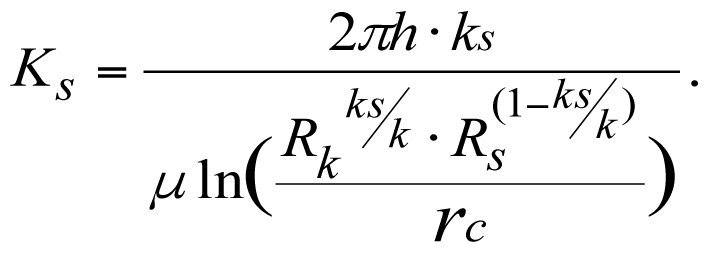  (3.25)

Коэффициент продуктивности K идеальной скважины

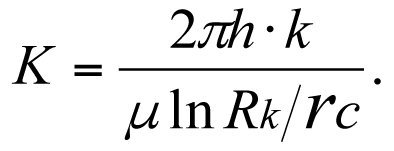(3.26)

Разделив (3.25) на (3.26), получим

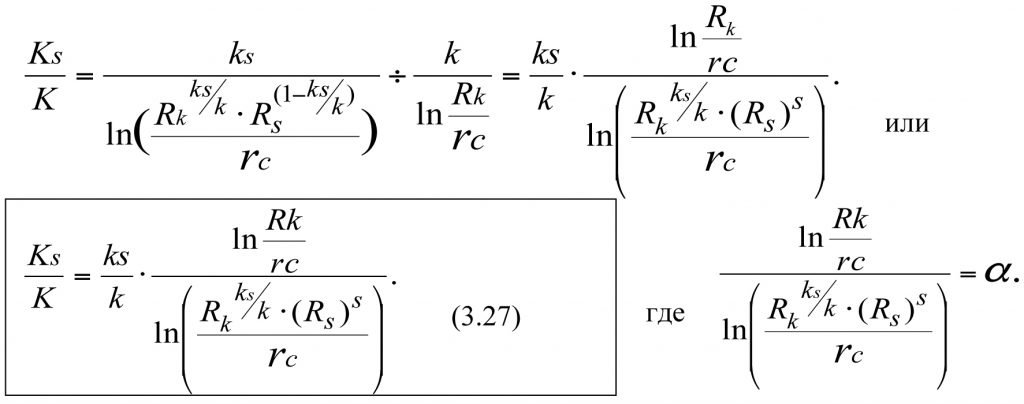  (3.27)   

Введем новое обозначение α, где α – коэффициент неоднородности пласта — коэффициент пропорциональности, учитывающий неоднородность пласта по проницаемости.         

С учетом формулы (3.16) запишем

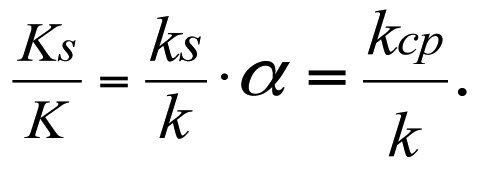 (3.28)

Из (3.28) следует важный вывод, что коэффициент продуктивности реальной скважины Ks прямо пропорционален среднему значению коэффициента проницаемости kср зонально-неоднородного пласта и относительные их величины равны между собой, а коэффициент проницаемости скин-зоны ks находится в прямой зависимости от коэффициента неоднородности пласта α.

3.3.2. Взаимосвязь между дебитом реальной скважины Qs и коэффициентом проницаемости ks. Рз-const; (Рз(k)=Pз(ks)).

Дебит реальной скважины                

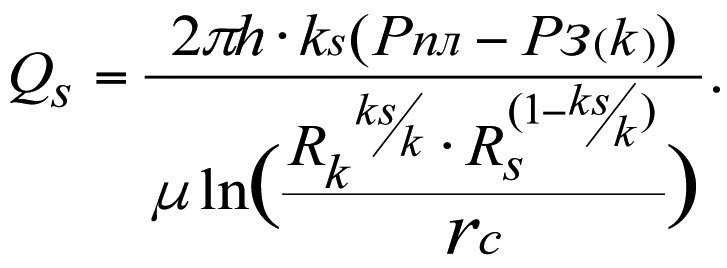
Дебит идеальной скважины

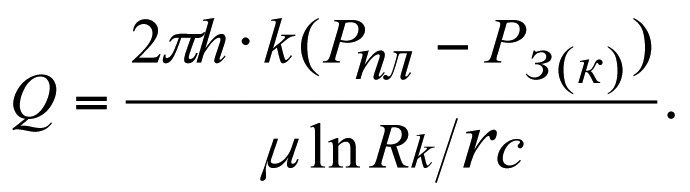
Разделив Qs на Q, получим

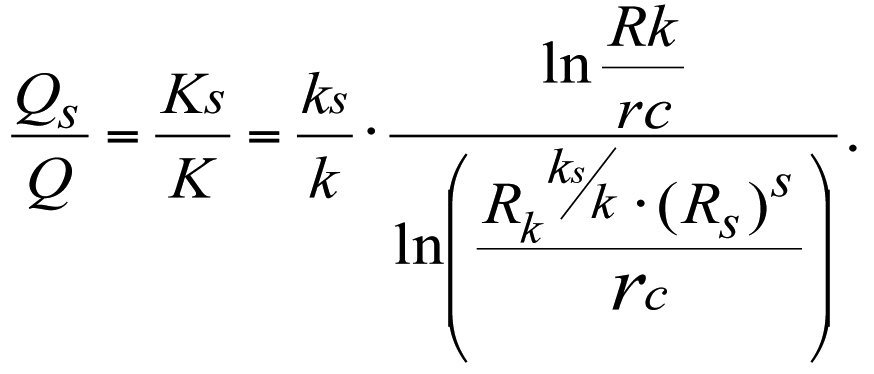    или

с учетом (3.16), запишем

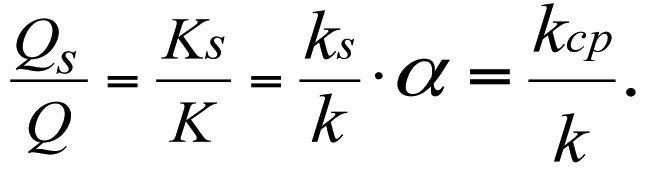 (3.29)

Формула (3.29) показывает, что дебит реальной скважины Qs прямо пропорционален значениям коэффициентов ks, Ks и kср, а относительные их величины равны между собой.                              

3.3.3. Взаимосвязь между коэффициентом проницаемости зонально-неоднородного пласта и падением пластового давления ΔΡks при фильтрации жидкости. Q-const.   

Потери пластового давления ΔΡk при фильтрации жидкости к забою идеальной скважины с коэффициентом проницаемости k пласта определяется формулой Дюпюи                                                         

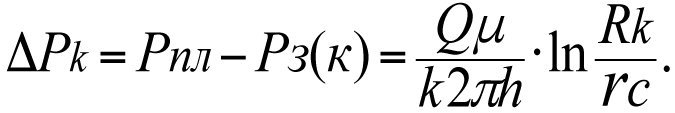
Общие потери пластового давления ΔΡks с учетом скин-слоя составят

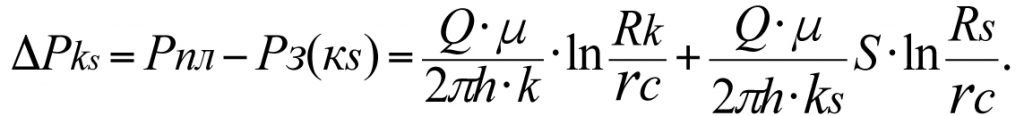
Разделив ΔΡk на ΔΡks, получим

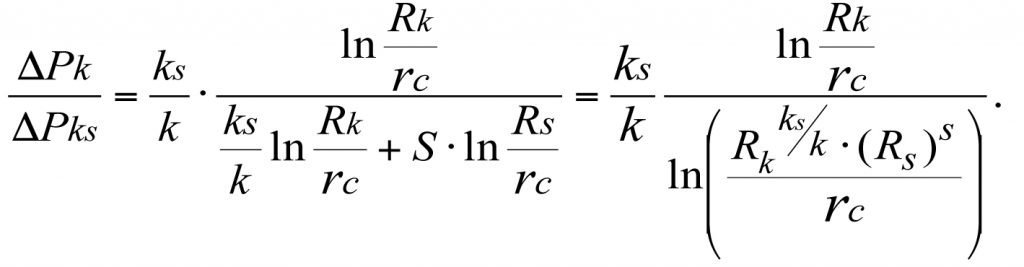
С учетом (3.16) и (3.29) имеем          

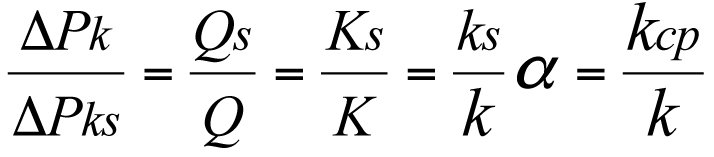  (3.30)

Из формулы (3.30) видно, что общие потери пластового давления ΔΡks в зонально-неоднородном пласте обратно пропорционально значениям Qs, Ks, ks и kср, а относительные их величины равны между собой

3.3.4. Взаимосвязь между потенциальным дебитом Qпот. неоднородного пласта и его коэффициентом проницаемости.

Потенциальный дебит реальной скважины с зональной неоднородностью пласта составит

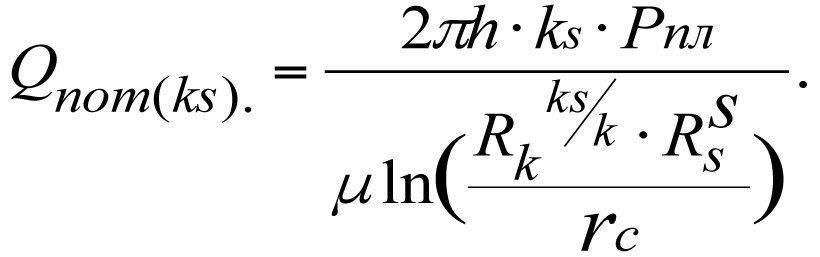
Потенциальный дебит идеальной скважины 

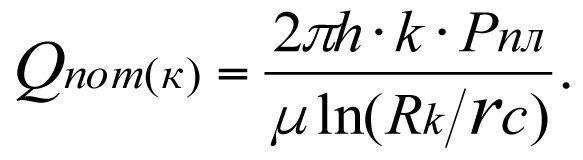
Разделив Qпот(ks) на Qпот(k), получим

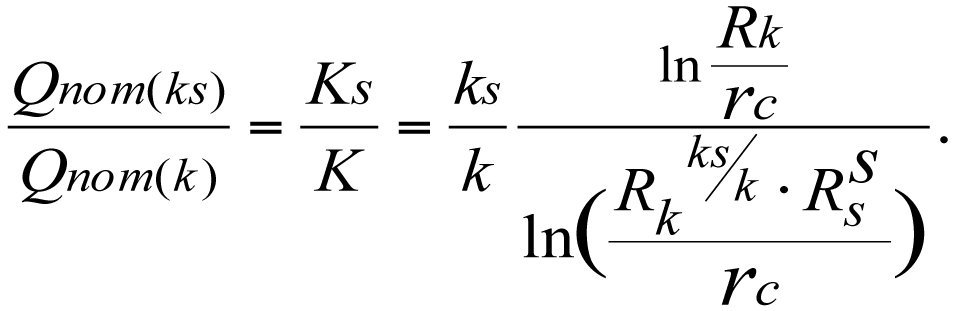
С учетом (3.16) и (3.30), запишем

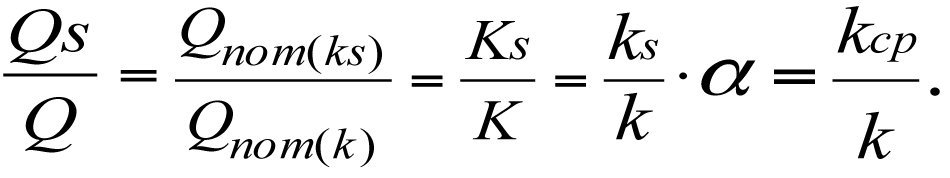(3.31)

Потенциальный дебит Qпот(ks) зонально-неоднородного продуктивного пласта находится в прямой зависимости от проницаемости kср, а относительные величины Q, Qпот, K, ks, kср равны между собой. 

3.4. Заблуждения и ошибки, допущенные в теории об эффективном (приведенном) радиусе rпр скважины.

Общепризнанные мнения о том, что каждый считает делом давно решенным,  чаще всего заслуживают исследования.
Георг К. Лихтенберг.
1742-1799.
    

По определению – приведенный радиус скважины r_пр – это радиус воображаемой, фиктивной гидродинамически совершенной скважины, дебит которой равен дебиту данной гидродинамически несовершенной скважины. Такое определение принято во всех научных и учебных изданиях, в т.ч. зарубежных, относящихся к гидродинамике нефтяного пласта. 

Из определения следует:

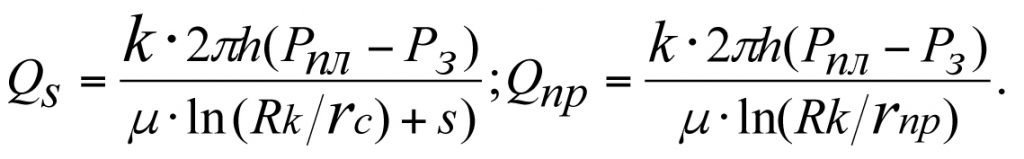
Поскольку дебиты двух скважин приравниваются при прочих равных условиях, имеем

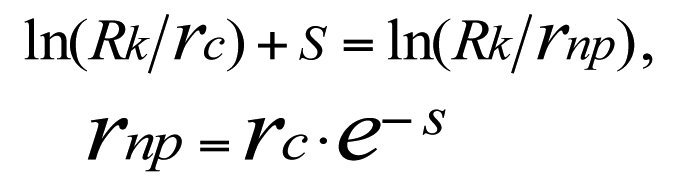    отсюда

   (х*)    

Несостоятельность определения приведенного радиуса и его формулы (х*) заключается в том, что теоретически существует бесчисленное множество гидродинамически совершенных фиктивных скважин с бесчисленными значениями приведенных радиусов, но равными дебитами, соответствующими дебиту одной гидродинамически несовершенный реальной скважины. Это хорошо иллюстрируется на рис. 3.2. и формулой (3.32).   Для формулировки приведенного радиуса и определения его значения условие равенства дебитов гидродинамически несовершенной реальной скважины и соответствующей ей гидродинамически совершенной фиктивной скважины является абсолютно несостоятельным и ошибочным условием.

Равные значения притока к забою бесчисленного множества фиктивных скважин с различными значениями приведенных радиусов, соответствующих значению притока к забою реальной скважины, можно получить при различных комбинациях с различными значениями коэффициента продуктивности Кi и забойного давления Pзi, т.е.депрессии ΔРi. См.рис. 3.2. и формулу (3.32).

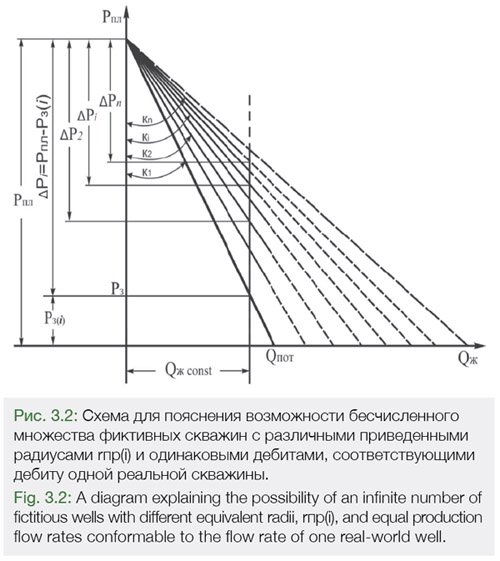
Бесчисленному множеству значений забойного давления Рз(i) соответствует бесчисленное множество значений коэффициента продуктивности К(i) и, соответственно, бесчисленное множество фиктивных скважин с различными приведенными радиусами rпр(i), но одинаковыми дебитами.

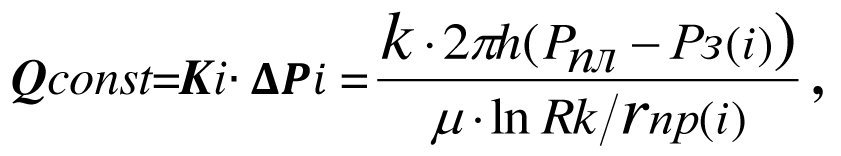(3.32)

3.4.1 Определение эффективного (приведенного) радиуса rпр скважины и вывод его формулы  

Одному значению коэффициента продуктивности Кconst соответствует бесчисленное множество комбинаций значений притока Qi и депрессии на пласт ΔРi, т.е.

Kconst = Qi/ΔPi, следовательно

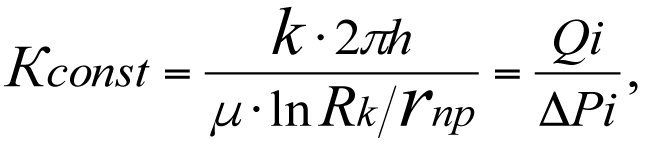(3.33)

где Qi – различные значения притока, соответствующие различным значениям депрессии ΔPi = Рпл — Рз(i) на пласт фиктивных скважин; rпр — приведенный радиус фиктивной скважины.      

Дебит реальной скважины с зональной неоднородностью пласта выразим через среднее значение коэффициента проницаемости kср (см. 3.16). При этом пласт рассматриваем как однородный с коэффициентом проницаемости kср.                                                        

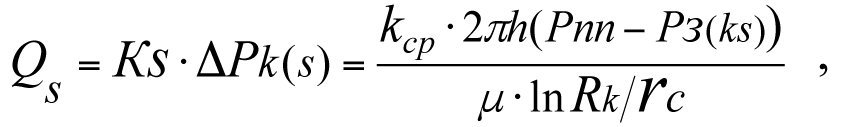  (3.34)   

Обозначения на рис. 3.2 и 3.3.

Дебит гидродинамически совершенной фиктивной скважины (кривая 1 на рис. 3.3.)                  

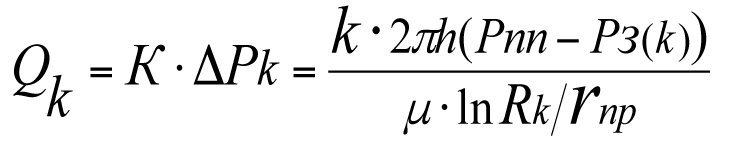(3.35)

При равенстве коэффициентов продуктивности Кs реальной и К фиктивной скважин (Кs=К),индикаторные линии Q=f(ΔP) этих скважин совпадут. При этом возможны различные варианты значений депрессии на пласт, (ΔРк>ΔРк(s)), (ΔРк<ΔРк(s)), (ΔРк=ΔРк(s)),соответствующие различным значениям притока Qi. При равенстве депрессии на пласт реальной и фиктивной скважин ΔРк=ΔРк(s),как частный случай, (см. рис. 3.2 и 3.3) будут равны и дебиты этих скважин.

Из формулы (3.33) видно, что одному значению коэффициента продуктивности соответствует бесчисленное множество комбинаций значений Qi и ΔPi, а эффективный (приведенный) радиус rпр привязан только к коэффициенту продуктивности К фиктивной скважины.

На основе анализа формул (3.33), (3.34) и (3.35) и рис. 3.2 и 3.3 можно сделать вывод о том, что при прочих равных условиях, единственному значению коэффициента продуктивности соответствует единственное значение эффектиного (приведенного) радиуса фиктивной скважины.        

Следовательно, определение эффективного (приведенного) радиуса скважины:

Эффективный (приведенный) радиус скважины — это радиус гидродинамически совершенной фиктивной скважины, коэффициент продуктивности которой равен коэффициенту продуктивности гидродинамически несовершенной реальной скважины.  

Равенство коэффициентов продуктивности реальной Кs и фиктивной К скважин является необходимым и достаточным условием для определения эффективного (приведенного) радиуса r_пр гидродинамически совершенной скважины.  

Дебит гидродинамически несовершенной (реальной) скважины из (3.34)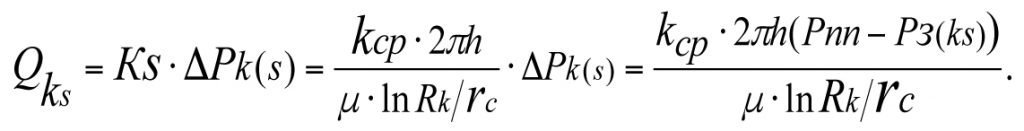  (3.36)              

Коэффициент продуктивности реальной скважины            

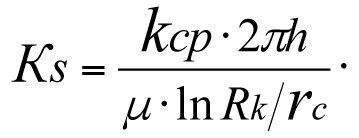   (3.37)

Дебит гидродинамически совершенной фиктивной скважины из (3.35)

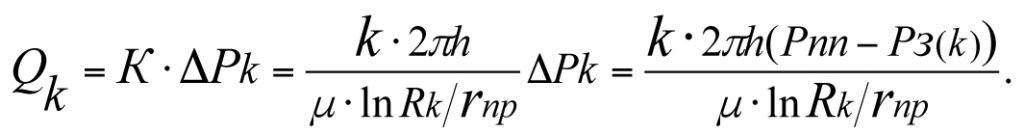  (3.38)

Коэффициент продуктивности фиктивной скважины           

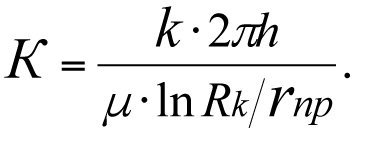(3.39)

При равенстве коэффициентов продуктивности реальной и фиктивной скважин, имеем

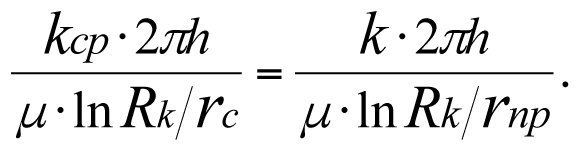(3.40)

Из (3.40) получим формулу для определения эффективного (приведенного) радиуса r_пр скважины

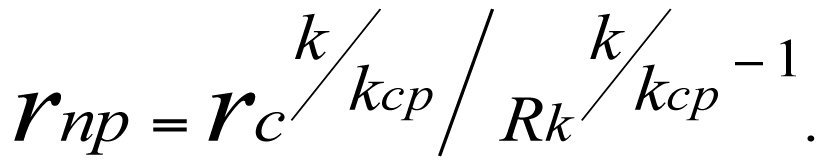  (3.41)

Среднее значение коэффициента проницаемости kср определяют по формуле (3.16).                  

Из (3.41) видно, что значение приведенного радиуса r_пр фиктивной скважины зависит от соотношения радиусов реальной скважины и контура питания в степенной зависимости. При равенстве коэффициентов проницаемости контура питания реальной и фиктивной скважин (т.е. при отсутствии скин — зоны, k=kср) радиусы этих скважин равны.

Послесловие от автора

Многогранная наука о подземной гидродинамики, охватывающая законов механики Ньютона и квантовой механики [9] не может быть логично завершена, ее можно лишь на время оборвать.

Проблемы, которые рассматривались в моих работах, относятся базовым положениям подземной гидродинамики. Исторические ошибки и заблуждения, допущенные в формулах для определения потери давления ΔР_s при фильтрации скважинной жидкости в околоскважинном пространстве, значения скин-фактора S, коэффициента продуктивности К и забойного Р_з давления, динамического уровня скважинной жидкости hд, текущего притока Qж, потенциального дебита Qпот и эффективного (приведенного) радиуса r_пр скважины – результаты ошибок одной цепочки. Негативные последствия этих ошибок и заблуждений нашли отражения в теории и практике основных положений ГДИС, ТИС и ГИС, но главные губительные последствия в том, что со второй половины прошлого столетия эти формулы без выводов и доказательств были включены во все учебники, учебные пособия и методические руководства соответствующего профиля вузов и курсов повышения квалификации.

Крайнее удивление вызывает тот факт, что ведущие идеологи гидродинамических исследований скважин Ипатов А.И., Кременецкий М.И., Гуляев Д.Н. [7] считают формулы V. Everdingen A. F. & Hurst N., 1949 (1*) и Hawkins M.F., 1956 (2*), составленные с нарушениями законов подземной гидродинамики и включающие грубые математические ошибки классикой и базовыми положениями ГДИС.

Формулы (1*) и (2*) для определения ΔРs , S, и (3.2), (3.2*), (3.3) и (3.3*) для расчета текущего дебита Qж, и эффективного (приведенного) радиуса r_пр (х*) скважины  не пригодны для расчета указанных базовых гидродинамических параметров реальной скважины с зонально-неоднородной проницаемостью пласта и должны быть исключены из учебников и учебных пособий подземной гидродинамики.

Фундаментальные зависимости гидродинамических параметров системы «Пласт-скважина — насосное оборудование» [9] должны быть использованы для проведения количественной оценки и полного анализа состояния пласта, геофизических, гидродинамических и технологических исследований (ГИС, ГДИС и ТИC), и всестороннего обоснования технологических и гидродинамических параметров при разработке программного обеспечения для инновационного проектирования процессов разработки нефтегазовых месторождений. 

Наука о подземной гидродинамики далека от совершенства и к концу 50-х годов практически полностью исчерпала свой потенциал и не создала ни одной фундаментальной теории, более того, сформировалась ошибочная концепция по базовым направлениям. Современная подземная гидродинамика больна изнутри. Основные причины болезни, ее живучести и устойчивости – глубокий застой научных идей в сочетании с догматическим подходом к формированию и решению фундаментальных научных проблем, и консерватизмом научного мышления. Исследовательские работы в области подземной гидродинамики с тех времен и по настоящее время свелись к разработке полуэмпирических подгоночных теорий, имеющих предварительный характер ошибочных концепций.

Вопросы подземной гидродинамики, на которые пока нет ответов

Продуктивный пласт находится под динамическим воздействием множеств геофизических (мульти) полей: геомеханического, гидродинамического, геомагнитного, электродинамического, геотермодинамического, гравитационного, волнового, оптического и их производных. Значения параметров этих геофизических полей находятся в полной взаимосвязи со всеми гидродинамическими параметрами пласта и зависят от пространственной неоднородности и временной изменчивости состояния всей системы [9].

Следующие положения подземной гидродинамики требуют ответов:

— установление законов фильтрация пластовой жидкости под воздействием геофизических мульти полей;

— установление влияния геофизических мульти полей на реологические параметры пластовой жидкости;

— установление взаимосвязи пластовой гравитации с электромагнитном и гидродинамическими полями пласта;

— установление взаимосвязи параметров всех геофизических (мульти) полей со всеми гидродинамическими параметрами пласта и их значениями;

— установление динамики (возрастания) энтропии пласта в процессе разработки месторождения.

На все эти вопросы, заданные природой можно получить ответы только в рамках законов квантовой механики.

Кроме того, на основе проведенных опытов И. Никурадзе над турбулентным движением жидкости установлена несоответствие результатов экспериментальных данных теоретическим в области вязкого подслоя пограничной зоны. Для устранения несоответствия введены эмпирические константы, как «дефект кинетической энергии», «дефект полного напора» и «дефект скорости». Эти дефекты могут быть устранены в рамках физики нелинейных процессов и квантовой механики. Следует отметить, что все классические законы сохранения имеют квантовый аналог, и обратно, есть квантовые законы сохранения, не имеющие аналога в классической физике.

Впереди научно-технического прогресса всегда идут фундаментальные идеи и открытия. Любые ошибки и заблуждения, допущенные в фундаментальных и базовых отраслях науки приводят в тупик, оборачиваются колоссальными издержками в процессе реализации, начиная от идеи и завершая технологическими циклами.

Автор выразит признательность за обоснованные и, аргументированные замечания и предложения, влияющие на структуру и содержание конечных формул и по уточнению определений.

Краткое сведения об авторе:

Robert Mufazalov

— 275 научных работ, из них:

— 117 изобретений;

— 13 монографий (научные книги);

— 4 учебников для вузов (с грифом минвуза);

— Заслуженный изобретатель Респ. Башкортостан;

— Изобретатель СССР;

— Отличник Министерства нефтяной промышленности  СССР;

— Включен в энциклопедию «Инженеры Урала»;

— Член-корреспондент РАЕН;

— Участник более 30 международных конференций, конгрессов и всемирных выставок по  новейшим и  наукоемким технологиям.

Научные интересы: квантовая геомеханика, подземная гидродинамика, гидравлика, нелинейная гидроакустика, техника и технология бурения, гидромеханика добычи нефти, нефтехимия, медицина — ( 8 патентов на изобретения), разработка и создание высоких технологий для нефтегазохимического комплекса.

Литература

1. Van Everdingen A.F., and Hurst W., «The Application of the Laplace Transformation to Flow Problems in Reservoirs», Trans. AIME, Vol. 186, 1949, pp. 305–24.

2. Hawkins M. F. Jr., «A note on the skin effect», Trans. AIME, Vol. 207, 1956, pp. 356–57.

3. Справочное руководство по проектированию разработки и эксплуатации нефтяных месторождений / Под общ. ред. Ш. К. Гиматудинова.– М.: Недра,1983. – 455с.

4. Ипатов А.И., Кременецкий М.И. Геофизический и гидродинамический контроль разработки месторождений углеводородов.- Изд. 2-е, испр.-М.: НИЦ «Регулярная и хаотическая динамика», 2010. – 780с.

5. Закиров С.Н., Индрупский И.М., Закиров Э.С. и др. Новые принципы и технологии разработки месторождений нефти и газа. Часть 2.-М.-Ижевск: Институт компьютерных исследований, НИЦ «Регулярная и хаотичная динамика», 2009. — 484с.

6. Щуров В.И. Технология и техника добычи нефти. Учебник для вузов. М.: Недра,1983, -510с.

7. Ипатов А.И., Кременецкий М.И., Гуляев Д.Н. Современные технологии гидродинамических исследований скважин и их возрастающая роль в разработке месторождений углеводородов//Нефтяное хозяйство.-2009.-№5.-С. 52-57.

8. Муфазалов Р.Ш. Скин-фактор. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта. Георесурсы. № 5. 2013. С. 34-48.

9. Mufazalov R.Sh. Fundamentals of Subsurface Hydrodynamics and a Quantum-Mechanical View of the Reservoir Model // «ROGTEC», Oil & Gas Magazine, issue 55, -рр. 44-59. (tel:+34 952 880 952,
editorial@rogtecmagazine.com).

10. Mufazalov R.Sh. Tim’s Theorem: A New Paradigm for Underground Hydrodynamics. Part 1 // «ROGTEC», Oil & Gas Magazine, issue 57, -рр. 62-78. (tel:+34 952 880 952, editorial@rogtecmagazine.com,).

11. Муфазалов Р.Ш. Скин-фактор и его значение для оценки состояния околоскважинного пространства продуктивного пласта.- Уфа: Изд-во УГНТУ, 2005.-44с.