Теорема Тима: Фундаментальная основа новой парадигмы подземной гидродинамики, Часть 1

«О нелокальности причин»
«Изолированных систем не существует, что вся система, даже разделенная на части огромными расстояниями, между которыми отсутствуют сигналы, поля, механические силы, энергии и т.д., функционируют как единая Система».
Джон Стюарт Белл 1928 — 1990.

Cтатья является продолжением публикаций [1,5,8…11], дополнением к ранее опубликованным работам по данной тематике и включает ответы на вопросы о потери давления, притока при фильтрации жидкости в зонально-неоднородном пласте, коэффициенте пропорциональности для базовых гидродинамических параметров, а так же о взаимосвязи и взаимозависимости основных гидродинамических параметров зонально-неоднородного пласта, заданные читателями публикаций и участниками конференций [3,5,6,9] в процессе обсуждения. В связи с этим, более подробно излагается вывод формулы для расчета  потери забойного давления ΔР_s, формулы скин-фактора S и других базовых гидродинамических параметров зонально-неоднородного пласта.

«Теорема Тима» гласит, что «Любые изменения проницаемости продуктивного пласта приводят к пропорциональному изменению его продуктивности, гидропроводности, забойного давления, динамического уровня жидкости, текущего притока и потенциального дебита, а безразмерные относительные их величины равны между собой».

Система «Продуктивный пласт – скважина — насосное (лифтовое) оборудование» — единая, неразделимая гидродинамическая система, взаимосвязанная фундаментальными зависимостями, отражающими единство и взаимосвязь всех гидродинамических параметров этой системы [4] (в дальнейшим — система).

Теорема Тима основана на трех фундаментальных взаимосвязанных законах подземной гидродинамики:

1. закон о пропорциональности базовых гидродинамических параметров системы [1,2].

В качестве коэффициента пропорциональности выступает значение Скин – фактора S;

2. закон о единстве, взаимосвязи и взаимозависимости базовых гидродинамических параметров системы [3], (ни один параметр системы, кроме независимых переменных: Р_пл и k,  самостоятельно не функционирует);

3. закон о равенстве между собой безразмерных относительных величин базовых гидродинамических параметров системы [5].

1. Вывод формулы для расчета потери давления ΔР_k при фильтрации жидкости в скважину

1.1. Аналитический вывод формулы для расчета потери давления ΔР_k при фильтрации жидкости (рис. 1.1).

Чтобы получить формулу для расчета потери пластового давления ΔР_k при филтрации жидкости, рассмотрим однородный продуктивный пласт вокруг стенки скважины с коэффициентом проницаемости k пласта, контура питания R_к, пластовым давлением Р_пл и мощностью пласта h (рис. 1.1).

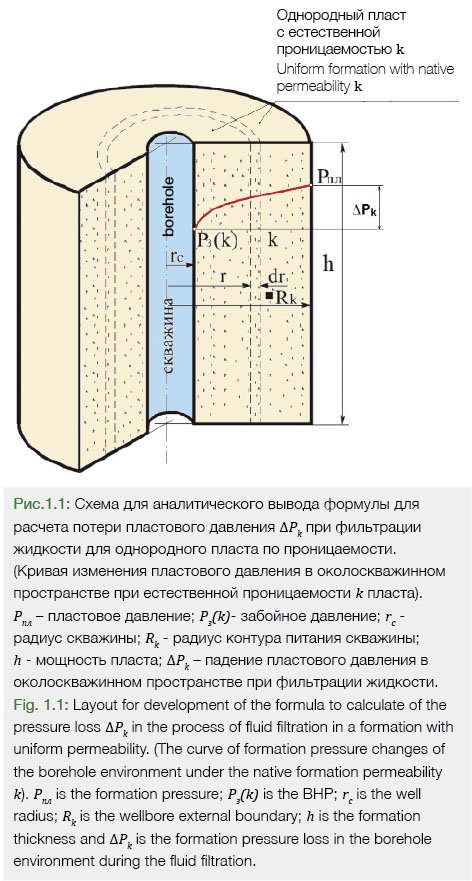
Выделим внутри пласта кольцевой слой с радиусом r и толщиной dr, ограниченной поверхностями с однородной проницаемостью k. Направление фильтрации жидкости – радиальное. В соответствии с линейным законом фильтрации общий объемный приток жидкости Q через единицу площади F равен

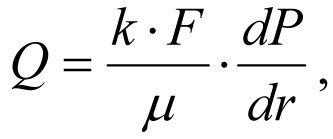 ,     (1.1)  где k – коэффициент

проницаемости;  F – площадь фильтрации жидкости, F=2πrh;  μ – динамическая вязкость пластовой жидкости; dP/dr – радиальный градиент давления.      Уравнение (1.1) перепишем в виде

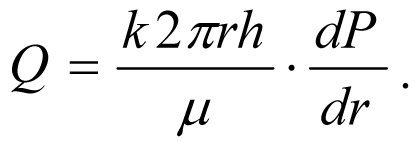 ,    (1.2)  Разделив переменные, запишем

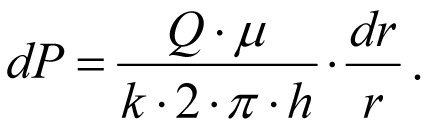 ,    (1.3)  Интегрирование этого уравнения дает

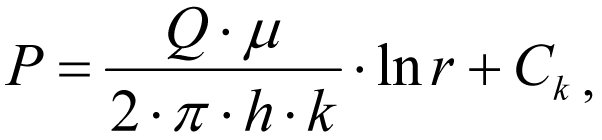 ,   (1.4)  где C_k – постоянная

интегрирования, зависящая от проницаемости пласта k, а 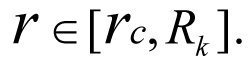 Чтобы  исключить C_k, подставляем значения переменных на границах стенки участка dr, а именно

r = R_к и r = r_c , в уравнение (1.4) и получим следующие два уравнения:

при r = R_к , получим пластовое давление т.е. Р=Р_пл

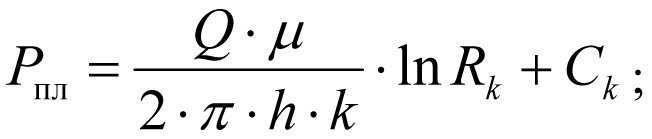(1.5)

а при r = r_c, получим забойное давление т.е. Р=Рз(k),

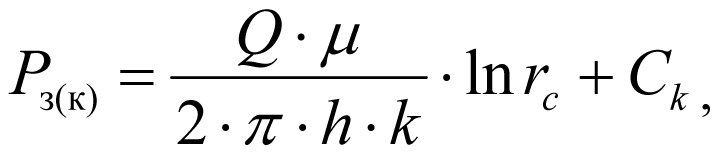 ,     (1.6)

где Рпл – пластовое давление, а Р_з(к) – давление у стенки скважины (забойное давление) при естественной проницаемости k пласта.

Вычитая из уравнения (1.5) уравнение (1.6), находим потери давления ΔР_k при фильтрации пластовой жидкости в скважину при естественной проницаемости k пласта

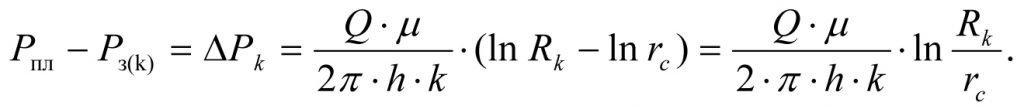
или

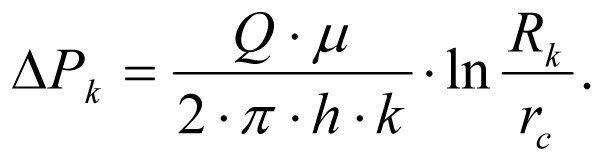 (1.7)                                        

Следовательно, ΔР_k — падение пластового давления при фильтрации жидкости в околоскважинном пространстве прямо пропорционально натуральному логарифму отношения радиуса контура питания пласта R_k к радиусу скважины r_c, и обратно пропорционально коэффициенту проницаемости k пласта.

Следует отметить, что вывод уравнения (1.7) аналогичен выводу уравнения теплопроводности цилиндрической стенки [4], а в теории однофазной фильтрации уравнение (1.7) называется формулой Дюпюи.

Уравнение (1.7) представляет собой уравнение логарифмической кривой, следовательно,  при фильтрации жидкости по пласту к скважине, падение давления ΔР_k изменяется по логарифмическому закону (рис. 1.1).

1.2. Вывод формулы для расчета  потери забойного давления ΔР_s при фильтрации жидкости в околоскважинном пространстве (в скин-зоне) реальной скважины

Van Everdingen A. F. и Hurst N. (1949) предложили формулу (1*) для расчета потери давления в околоскважинном пространстве при фильтрации жидкости в скважину [12].

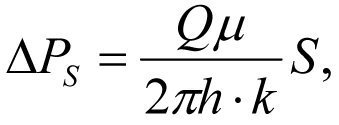 (1*)      

где ΔР_s — дополнительные потери пластового давления при фильтрации жидкости в скважину из-за ухудшения проницаемости пласта в скин-слое от k до ks; µ — динамическая взякость пластовой жидкости Q;  S — значение скин-фактора.

Следует отметить, что аналитический вывод выражения (1*) не существует (и не может существовать!), кроме того, в формуле (1*) для расчета ΔР_s допущены грубые ошибки [1,3,11], где не соблюдены физические законы гидродинамики пласта, нарушена математическая логика и допущены указанные серьезные ошибки. Hawkin M.F.(1956), используя (1*), предложил для расчета скин-фактора S формулу:

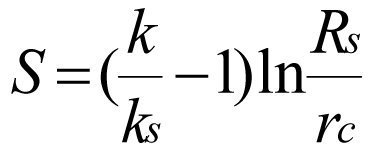 (2*), вошедшую в учебную и научную литературу, как Hawkins’ formula [13]. 

Согласно этой формуле, S может принимать значения  от минус бесконечности до нуля и от нуля до плюс бесконечности т.е.     ,

без принадлежности области определения, существования и практического использования. Известно, если функция стремится к бесконечности, она практического применения не имеет. Формулы (1*) и (2*) не пригодны для определения ΔР_s, S и других базовых параметров, входящих в систему и должны быть исключены из учебников и учебных пособий подземной гидродинамики. Параметры ΔР_s и S имеют важное значение и входят в состав формулы всех базовых гидродинамических параметров системы зонально-неоднородного пласта. В связи с этим в данной работе в четырех вариантах приводится вывод формулы для расчета значения ΔР_s и в пяти вариантах приводится вывод формулы для расчета значения скин-фактора S. 

Для дальнейших рассуждений логарифмическую кривую падения пластового давления из рис. 1.1 перенесем на рис. 1. 2  кривая 1).

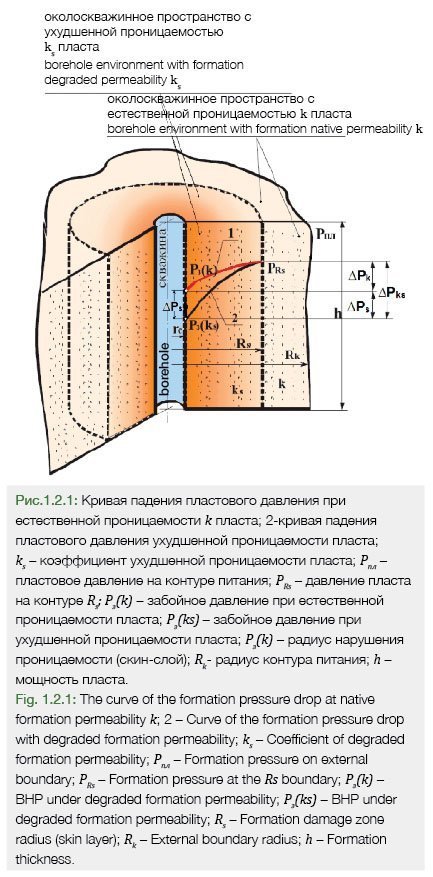
Ухудшение проницаемости околоскважинного пространства от k до k_s на величину ∆k приводит к снижению забойного давления от Р_з(k) до Р_з(ks) на величину ∆Рs (рис. 1.2), где Рз(k) – забойное давление при естественной проницаемости k пласта (забойное давление идеальной скважины), а Рз(ks) – забойное давление при ухудшенной проницаемости ks пласта (забойное давление реальной скважины). Давление пласта на  контуре R_s равно Р_Rs.  Кривая 1 характеризует потери пластового давления при фильтрации жидкости в околоскважинном пространстве с естественной проницаемостью k пласта, следовательно, уравнение (1.7) примет вид (для идеальной скважины)        

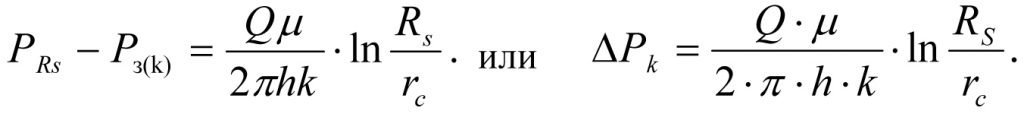
(1.8)

Кривая 2 характеризует потери пластового давления при фильтрации жидкости с ухудшенной проницаемостью пласта k_s, т.е. в скин-зоне, следовательно, уравнение (1.8) примет вид (для реальной скважины)                    

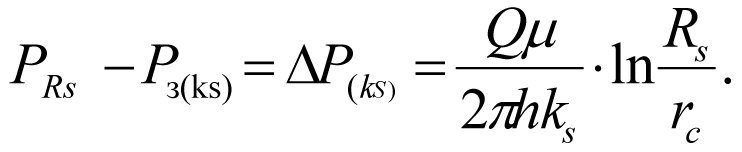  (1.9)      

Потери забойного давления на величину ΔР_s, полученный разностью значений между Р_з(к) и Р_з(кs)  (см. рис. 1.2), является результатом скин–фактора S, т. е.

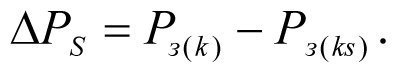  (1.10)

Падение давления на величину ∆Р_(ks) в скин-слое составит (см. рис.1.2 и формулу (1.9))

 (1.11)

Падение забойного давления на величину ΔРs  пропорционально скин-фактору S, т.е. ΔРs это дополнительное фильтрационное сопротивление из-за ухудшения проницаемости пласта в реальной скважине от k до k_s, следовательно,      

  (1.12)

Пользуясь уравнениями (1.9) и (1.12), запишем падение забойного давления ΔРs для зонально-неоднородного пласта в результате нарушения его проницаемости от k до k_s

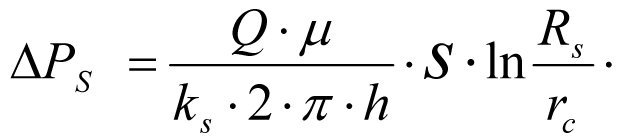 (1.13)              

Уравнение (1.13) получено автором в 2003г.и опубликовано в 2005г.[7] и является ключевым уравнением для расчета всех базовых гидродинамических параметров системы зонально-неоднородного пласта реальной скважины.

1.3. Вывод формулы ∆P_s для зонально-неоднородного пласта с учетом потери давления в интервале контура питания (R_k-R_s)  и в скин-слое (R_s-r_c) (см. рис.1.3).

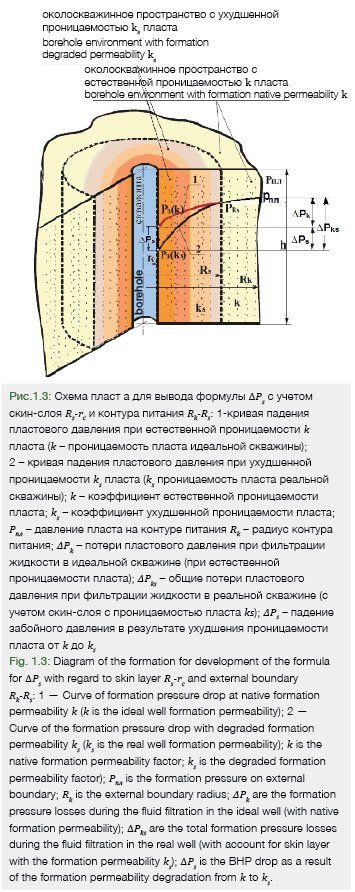
Более привлекательным является вывод формулы для расчета ∆P_s с учетом потери давления при плоскорадиальной фильтрации пластовой жидкости в зонально-неоднородном (по проницаемости) пласте в интервале контура питания (R_k-R_s) с проницаемостью пласта k и в скин-слое  (R_s-r_c) с проницаемостью k_s.

На участке [R_k-R_s] коэффициент проницаемости равен k, поэтому можно воспользоваться формулой (1.4), из которой находим при r = R_k  и  r = R_s :

при r = R_k , получим пластовое давление Рпл:             

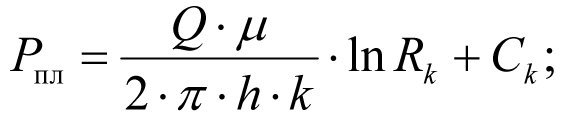 (1.17)                                                                               

а при r = R_s, получим давление на контуре R_s, равное РR_s,

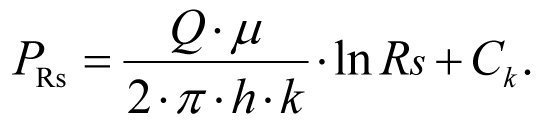    (1.18)

Вычитая из уравнения (1.17) уравнение (1.18), находим потери давления  на участке [R_k-R_s] с проницаемостьюk:                      
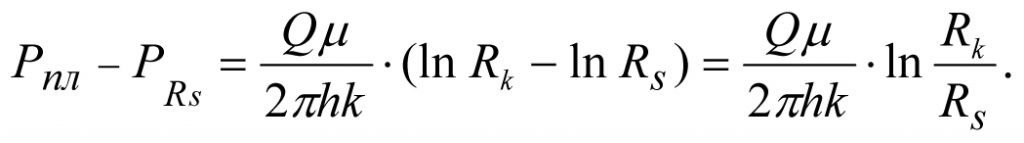    (1.19)   

На участке  [R_s-r_c] коэффициент проницаемости равен k_s,  а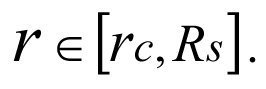  

Подставив в общую формулу (1.4) вместо k значение k_s, r = r_c и r = R_s, при r = r_c, будем иметь забойное давление

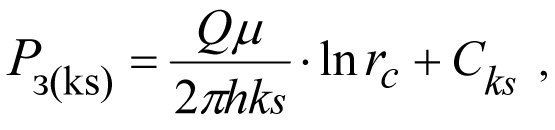 (1.20)

где  — постоянная интегрирования, соответствующая коэффициенту проницаемости k_s.
а при r = R_s, получим давление на контуре R_s,               

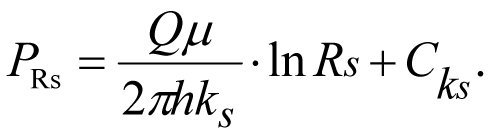    (1.21)

Вычитая из (1.21) уравнение (1.20), находим потери давления в скин-слое с  проницаемостью k_s :                                                       

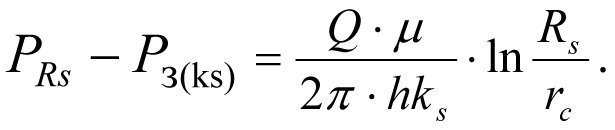   (1.22)                                             

Суммируя (1.19) и (1.22), находим потери давления в зонально-неоднородном интервале пласта [R_к, r_c]: 

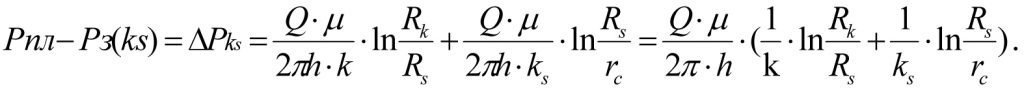         или

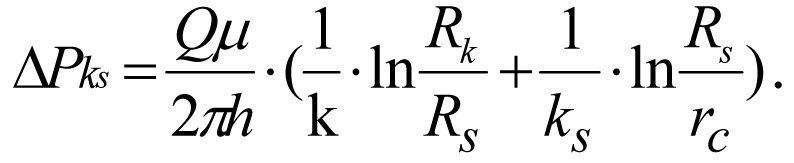    (1.23)                                                                                                                                         

Потери давления в околоскважинном пространстве при естественной проницаемости k пласта (кривая 1) составят

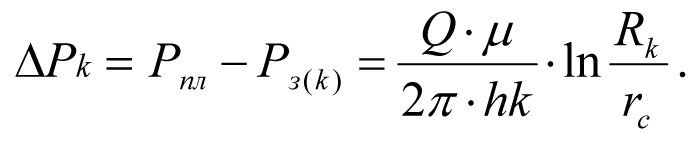 (1.24)

Вычитая  (1.24) из (1.23) получим формулу для расчета потери забойного давления ∆Ps при фильтрации жидкости в зонально-неоднородном пласте (см. рис.1.3).

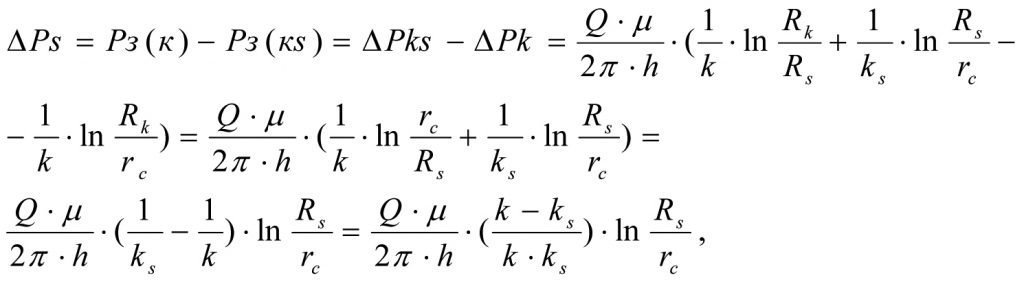                                                         или     

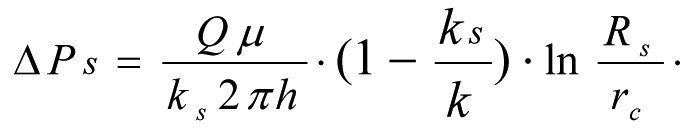 (1.25)

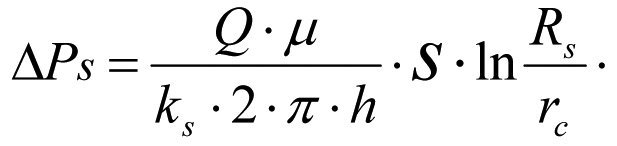       (1.26)

1.4. Вывод формулы для расчета ∆P_s для зонально-неоднородного пласта при постоянном дебите (Qж-const) (рис.1.3)

Потери давления в околоскважинном пространстве при естественной проницаемости k пласта (кривая 1) составят

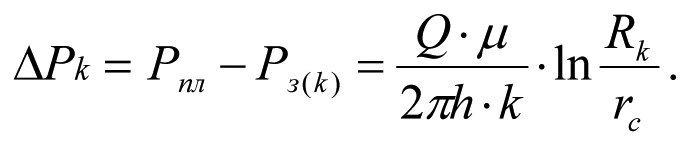 (1.27)            

При этом общий перепад давления в зонально-неоднородном пласте составит

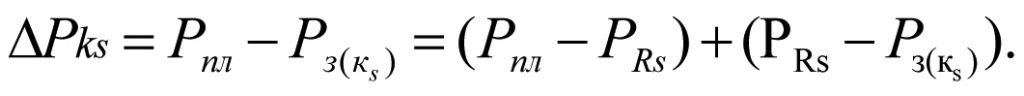  (1.28)

Потери давления в контуре питания с проницаемостью k составит

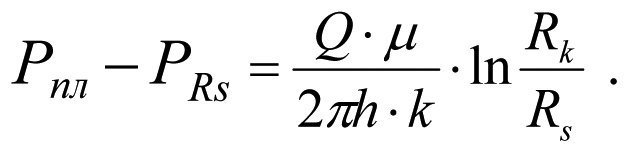  (1.29)

Потери давления в скин-слое с проницаемостью k_s составит

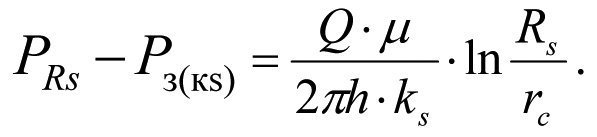  (1.30)

Подставляя значения (1.29) и (1.30) в (1.28), получим потери давления при плоско-радиальной фильтрации жидкости в зонально-неоднородном пласте по проницаемости

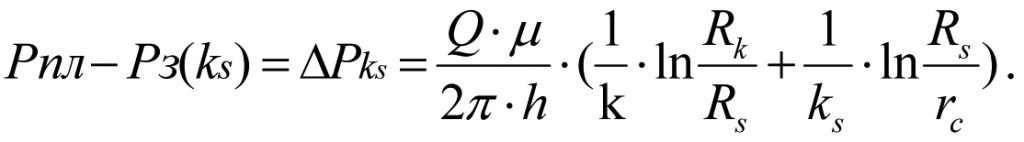
(1.31)

Вычитая (1.27) из (1.31), получим дополнительные потери давления ∆P_s в скин-слое в результате ухудшения проницаемости от k до ks (см. рис. 1.3).

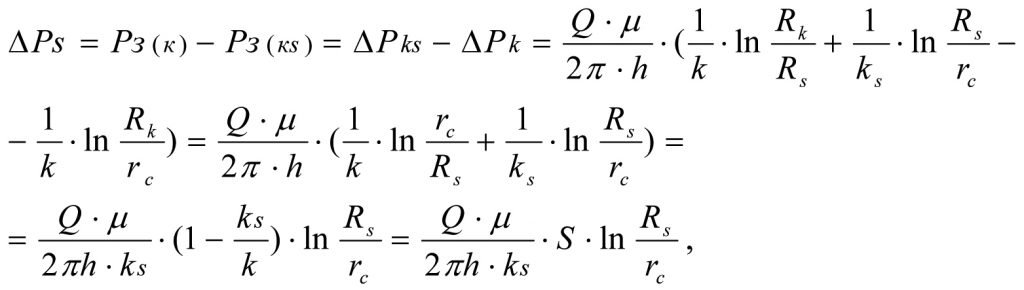
или

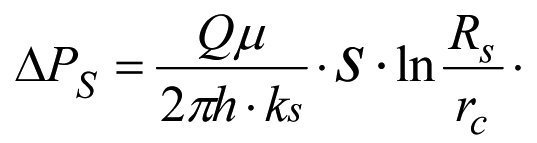      (1.32)                                       

Формулы (1.13), (1.26) и (1.32), полученные различными способами —  идентичные.

2. Вывод формулы для расчета скин-фактора S

Подробный аналитический вывод формулы для расчета скин-фактора S приведен в работах[1,2,8]. Аналитический вывод формулы для расчета скин-фактора S подтверждается выводами через индикаторные линии «дебит – давление», «дебит – уровень», а также по значениям забойного давления и потенциального дебита.

2.1 Вывод формулы скин-фактора S для зонально-неоднородного пласта, т.е. с учетом потери давления в контуре питания скважины (R_k-R_s) и скин-слое (R_s-r_c) (см. рис.1.3).

Падение пластового давления при фильтрации жидкости к забою идеальной скважины составит (1.24)

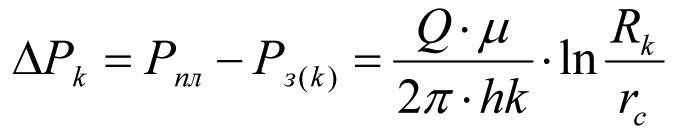
Потери пластового давления при плоско-радиальной фильтрации жидкости в зонально-неоднородном пласте по проницаемости составит (1.23)

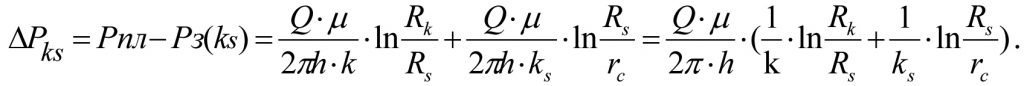
Вычитая  (1.24) из (1.23) получим потери давления ∆P_s в скин-слое (см. рис. 1.3)

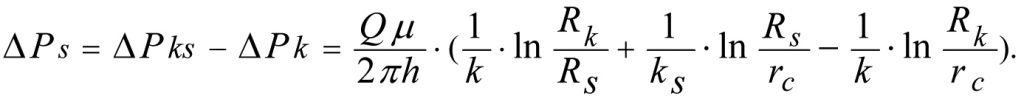
(2.1)

Падение забойного давления в результате нарушения проницаемости в скин-слое от k до ks составит (1.13)                           

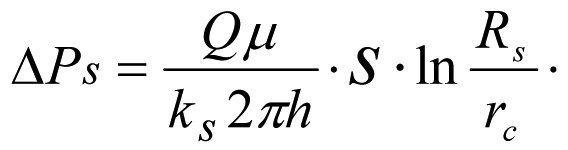  (2.2)

Приравнивая правые части (1.28) и (1.29) получим формулу скин-фактора

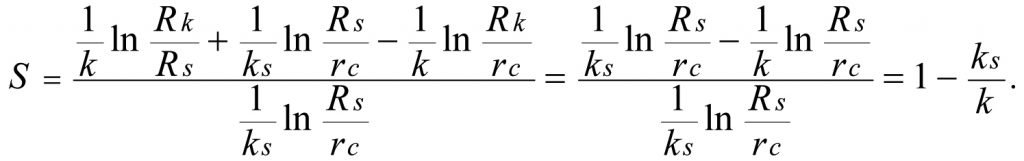
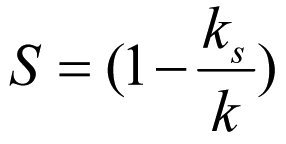   (2.3)

2.2. Вывод формулы скин-фактора S через индикаторные линии «дебит-давление» при Р_з=const и h_д=const (рис. 2.1)

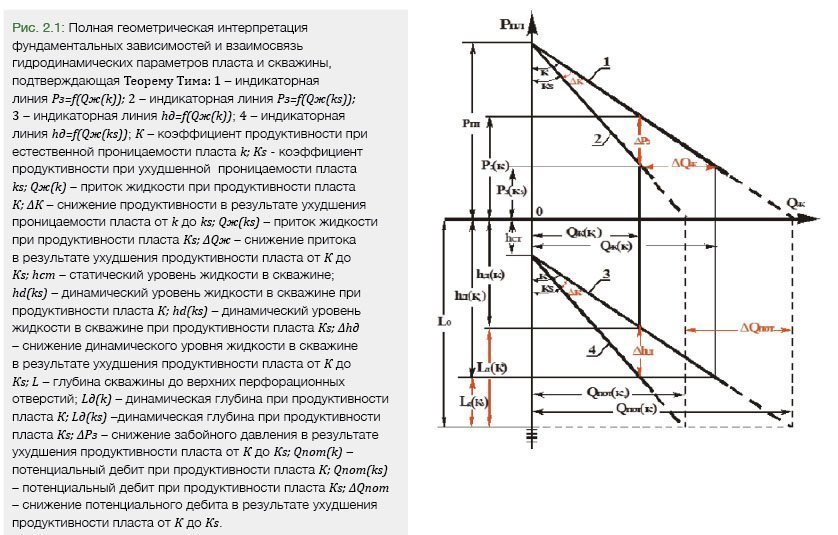
При равенстве забойных давлений идеальной и реальной скважин объемный приток (дебит) жидкости зависит только от коэффициента продуктивности скважин, при этом

Рз(кs)= Pз(к)= Рз;  Рпл-Рз(кs)=Рпл-Рз(к)=Рпл-Рз=ΔРconst.

Приток жидкости к забою идеальной скважины при естественной продуктивности пласта К составит                       

Qж(к)=К . ΔΡ   (2.4)

Приток к забою реальной скважины при ухудшенной продуктивности пласта К_s

Qж(ks) = Ks . ΔР.    (2.5)

Снижение притока жидкости ΔQ_ж в скважину в результате ухудшения продуктивности пласта от К до К_s составит             

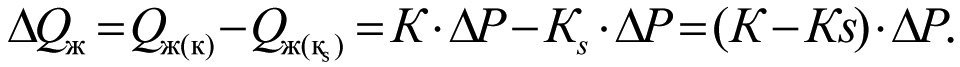  (2.6)                                    

Так как снижение притока жидкости в скважину пропорционально скин-фактору, введем обозначение

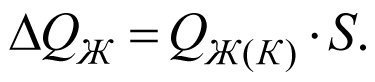 (2.7)        

Подставляя (2.4) и (2.6) в (2.7), получим (2.8)

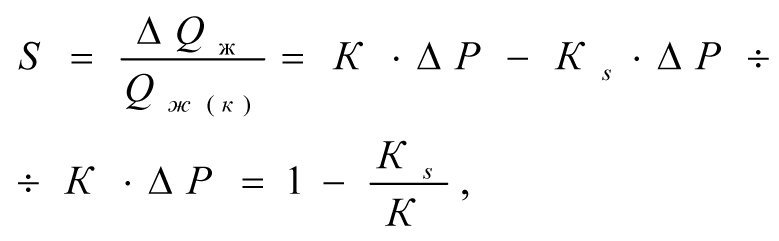   (2.8)

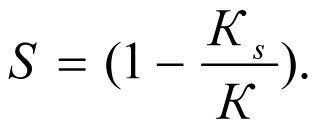 (2.9)

2.3.  Вывод формулы скин-фактора S через индикаторные линии «дебит-уровень» при Q_ж const  (рис. 2.1)

Приток жидкости Q_ж к забою при естественной продуктивности пласта K составит

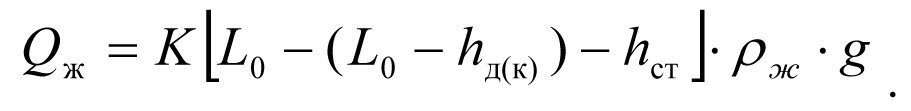 (2.10)

При постоянстве отбора жидкости ухудшение  продуктивности от К до К_s приводит к снижению динамического уровня от hд_(к) до hд_(кs), следовательно:

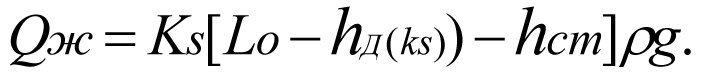 (2.11)

Пользуясь (2.10) и (2.11), определим динамические уровни при коэффициентах продуктивности К и К_s:

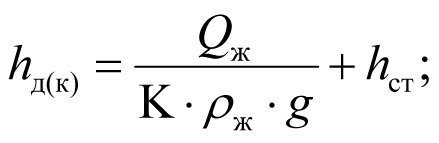 (2.12)              

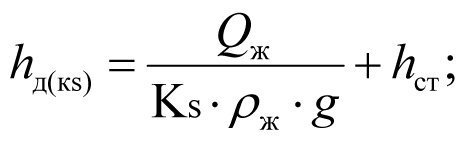 (2.13)

Падение динамического уровня Δh_д составит

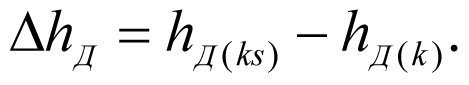 (2.14)

Подставляя значения (2.12) и (2.13) в (2.14), получим

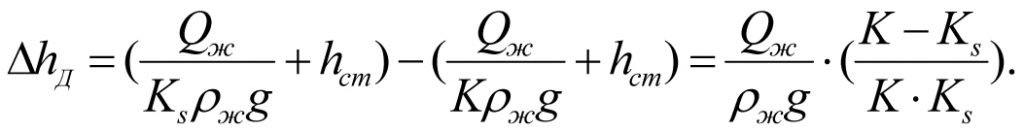  (2.15)

Падение динамического уровня на величину Δh_Д  пропорционально скин-фактору S, введем обозначение                                         

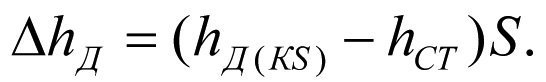   (2.16)       

Пользуясь уравнением (2.13), запишем

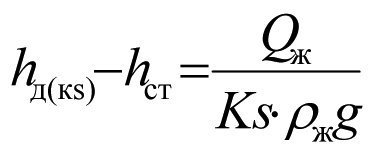 (2.17)

После подстановки (2.15) и (2.17) в (2.16) получим

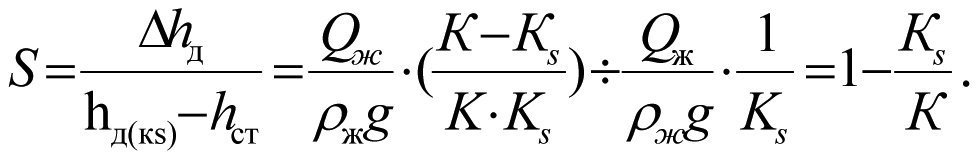 или

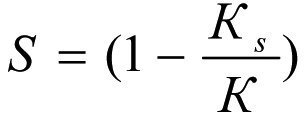 (2.18)

2.4. Вывод формулы скин-фактора S по значению забойного давления при Q_ж — const  (рис. 2.1)

Уравнение притока жидкости Q_ж при значениях продуктивности К и К_s, запишем в виде                                                                                      

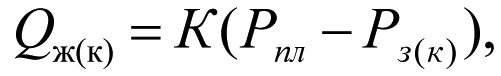  (2.19)

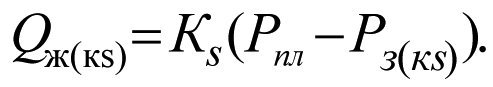   (2.20)

Из формулы (2.19) определяем забойное давление Р_з(к) при естественной продуктивности К пласта                         

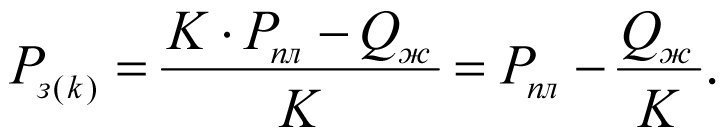 (2.21)

Из формулы (2.20) определяем забойное давление Р_з(кs)  при ухудшенной продуктивности пласта К_s ,т.е. при наличии скин — зоны

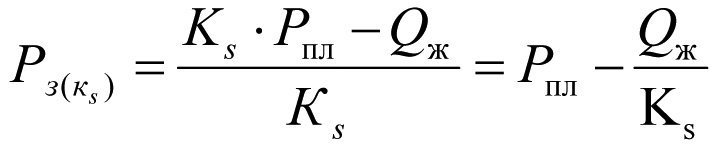    (2.22).   

При постоянстве отбора жидкости ухудшение продуктивности пласта от К до К_s приводит к падению забойного давления от Р_з(к) до Р_з(кs).

Падение забойного давления Δ_Рз составит

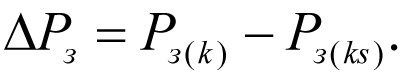 (2.23)                   

Подставляя значения Р_з(к) и Р_з(кs) в (2.23), получим

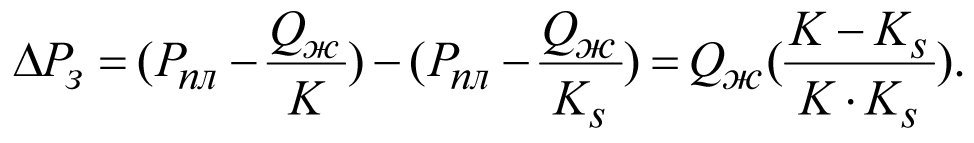                                                              (2.24)

Падение забойного давления на величину Δ_Рз пропорционально скин-фактору S.

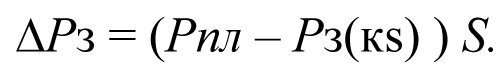 или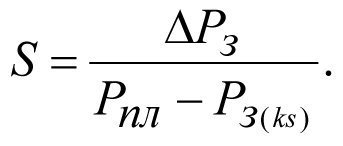                                 

(2.25)

Из формулы (2.20) запишем

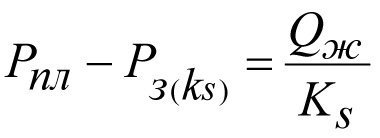 (2.26)

Подставляя значения из (2.24) и (2.26) в (2.25), получим

или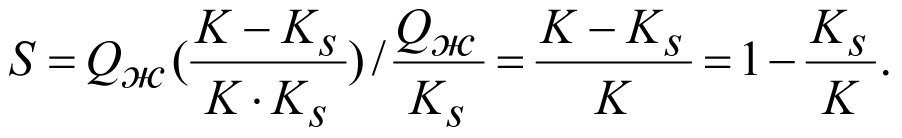      

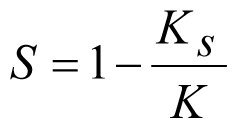(2.27)

2.5. Вывод формулы скин–фактора S по значению потенциального дебита (рис. 2.1)

Потенциальным дебитом скважины называют дебит, который может быть получен при Р_з=0. Динамический уровень скважинной жидкости при этом снижается до верхних перфорационных отверстий т.е. h_д=L₀. Пластовое давление остается без изменения,

Р_пл — const.

Из уравнения притока потенциальный дебит при коэффициенте продуктивности К составит

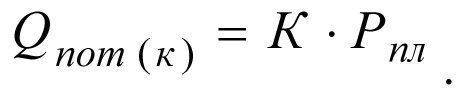 (2.28)

При наличии скин–слоя коэффициент продуктивности падает от К до К_s, тогда потенциальный дебит составит          

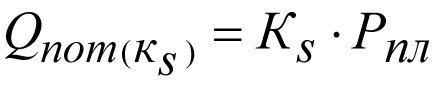(2.29)

Снижение потенциального дебита  ΔQ_пот в результате ухудшения продуктивности пласта от К до К_s составит

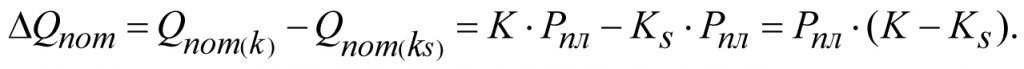
(2.30)

Снижение потенциального дебита на величину  ΔQ_пот пропорционально скин–фактору S,                                                            
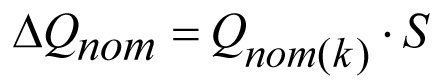 или 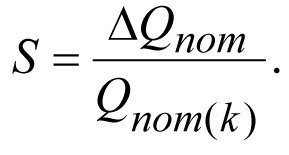 (2.31)

Подставляя значение (2.28) и (2.30) в (2.31), получим

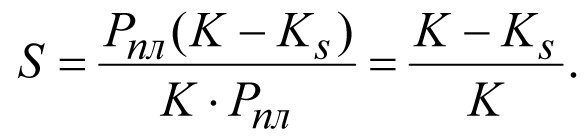
или 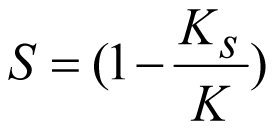  (2.32)

Формулы (2.3) и (2.9) для расчета значения скин-фактора S, выведенные через коэффициентов проницаемости k и продуктивности К идентичные и можно сделать следующие выводы:

— числовое значение скин-фактора S показывает долю ухудшения естественной проницаемости пласта и не имеет логарифмическую природу (логарифм под знаком s является результатом исторической ошибки);    

— числовое значение скин–фактора S представляет безразмерную величину;

— числовое значение  скин–фактора S имеет только положительную величину (отрицательное значение s является результатом заблуждения исторической ошибки), т.к. коэффициент проницаемости идеального пласта k всегда больше коэффициента проницаемости скин-зоны ks, т.е. k >ks;

— область определения S (принадлежность),  S ∈ (0,1];

— область существования S, 0<S≤1;

— при равенстве значений ks=k или К_s=К скин –

фактор S отсутствует (случай, когда пласт не имеет нарушений),

— при ks=0 или К_s=0 скин–фактор S принимает максимальное значение, т. е. S=1 (случай, когда пласт абсолютно непроницаемый).

Скин-фактор – комплексный параметр, отражающий интегрально все виды механизмов нарушения коллектора, влияющих на ухудшение проницаемости и пористости околоскважинного пространства продуктивного пласта и на снижение притока пластовой жидкости.

Скин-фактор вносит свой огромный негативный вклад на всех этапах жизни месторождения — начиная от проектирования разработки и завершая его списанием:

— в стадии проектирования разработки месторождения скин-фактор закладывается в виде допущенных ошибок проектирования;

— в стадии строительства и разработки месторождения скин-фактор обеспечивается в виде реализованных ошибок проектирования;

— в стадии эксплуатации месторождения скин-фактор реализуется в виде огромных невозобновляемых затрат на эксплуатацию месторождения с необратимыми нарушениями параметров пласта и на восстановление разрушенной гидрогеоэкологии.

Продолжение следует

Литература

1. Муфазалов Р.Ш.  Скин-фактор. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта.  Георесурсы. № 5. 2013. С. 34-48.

2. Муфазалов Р.Ш. Скин-фактор и его значение для оценки состояния околоскважинного пространства продуктивного пласта. // Научно-технический журнал «Технологии ТЭК» №3(34). 2007. С.36-42.

3. Муфазалов Р.Ш. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта при выводе формулы Скин-фактора. // Материалы международной научно-практической конференции «Инновационные технологии в геологии и разработке углеводородов». Казань: Изд-во НПО «Репер». 2009. С.303-310.

4. Михеев М. А. Основы теплопередачи: Учебник для вузов. –М.: Госэнергоиздат,     1949.-   396с.

5. Муфазалов Р.Ш. Скин-Фактор. Фундаментальные зависимости параметров пласта, скважины и оборудования. // Материалы международной научно-практической конференции «Актуальные вопросы разработки нефтегазовых месторождений на поздних стадиях». Уфа: Изд-во УГНТУ. 2010. С.80-93.

6. Муфазалов Р.Ш. Исторические ошибки и заблуждения, допущенные в теории гидродинамики нефтяного пласта и их последствия. Часть 1, 2, 3. // Труды 12 — Международного симпозиума «Энергоресурсоэффективность и энергосбережение». Казань: «Центр Оперативной Печати». 2011. С.409-464.

7. Муфазалов Р.Ш. Скин-фактор и его значение для оценки состояния околоскважинного пространства продуктивного пласта. Уфа: Изд-во УГНТУ. 2005. 44 с.

8. Mufazalov R.Sh. SKIN FACTOR and its importance for evaluating borehole environmental conditions for a productive formation. // «ROGTEC», Oil & Gas Magazine. Is. 19. Р. 18-36.

9. Муфазалов Р.Ш. Теорема Тима. Фундаментальные зависимости гидродинамических параметров пласта и скважины, и их взаимосвязь – основа инновационного проектирования процессов разработки нефтегазовых месторождений. // Материалы Международной научно-практической конференции «Моделирование геологического строения и процессов разработки – основа успешного освоения нефтегазовых месторождений». – Казань: Изд-во «Слово», 2018. с. 67 – 69.

10. Mufazalov R. Sh. Skin-Factor. Fundamental Relationships and interrelations Relationships, Conclusions and the Formula for the Key Hydrodynamic Parameters. // «ROGTEC», Oil & Gas Magazine. Is. 41. Р. 74-88.

11. Mufazalov R. Sh. Fundamentals of Subsurface Hydrodynamics and a Quantum-Mechanical View of the Reservoir Model. // «ROGTEC», Oil & Gas Magazine. Is. 55. Р. 42-57.

12. Van Everdingen A.F., and Hurst W., «The Application of the Laplace Transformation to Flow Problems in Reservoirs», Trans. AIME, Vol. 186, 1949, pp. 305–24.

13. Hawkins M. F. Jr., «A note on the skin effect», Trans. AIME, Vol. 207, 1956, pp. 356–57.

Author:  Муфазалов Р. Ш., Научно-производственная фирма «Пакер», г. Октябрьский, РБ